Science Forum: Best practices to promote rigor and reproducibility in the era of sex-inclusive research
- Division of Women’s Health, Department of Medicine, Brigham and Women’s Hospital and Harvard Medical School, United States
- Department of Epidemiology, Harvard TH Chan School of Public Health, United States
- Department of Psychology, Emory University, United States
- Radcliffe Institute for Advanced Study, Harvard University, United States
Figures
Figure 1
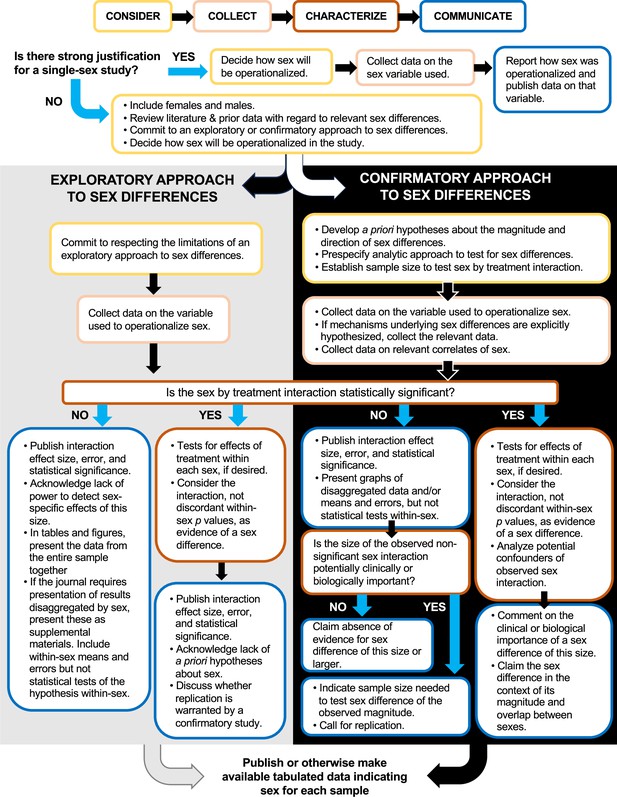
Exploratory and confirmatory research in the “4 Cs” framework for studying sex.
Decision tree depicting how the “4 Cs” framework can be applied to either an exploratory or confirmatory approach to testing for sex differences. Best practices are shown for testing for a sex difference in a treatment effect (or exposure-outcome association). For observational studies, “exposure” should be substituted for “treatment”.
Figure 2
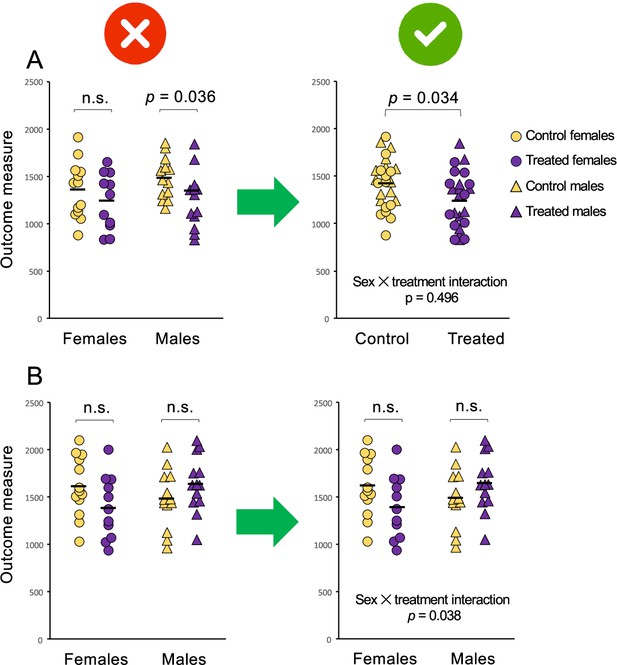
Analysis of data separately by sex can lead to erroneous conclusions.
The graphs above show the response to a control (yellow) or experimental (purple) treatment in females (circles) and males (triangles). Solid black lines represent the mean within each group. The top two graphs (A) depict two different approaches to the same dataset, in which there is an effect of treatment irrespective of sex and no sex difference in the response to treatment. The left panel shows how analyzing the data separately by sex, that is, making the difference in sex-specific significance (DISS) error (Maney and Rich-Edwards, 2023), leads to a false positive finding of a sex difference. The effect of treatment is statistically significant for males (*P=0.036) but not for females (P=0.342) but concluding a sex difference in the response to treatment constitutes an error – the sexes have not been compared statistically. To compare the responses between males and females, we can test for an interaction between sex and treatment, for example in a two-way analysis of variance (ANOVA). The sex × treatment interaction is not statistically significant (P=0.496), meaning there is no evidence that males and females responded differently and no justification to test for effects of treatment separately within each sex. The main effect of treatment, which is estimated from all subjects combined, is significant (P=0.034) suggesting that the treatment altered the outcome measure irrespective of sex. To communicate the main effect of treatment, which is the important finding in this case, the sexes are combined for presentation (right panel). The bottom two graphs (B) depict two approaches to a different dataset, in which there is no main effect of treatment but the sexes did respond differently. The effect of treatment is not statistically significant within females (P=0.115) or within males (P=0.185), so separate analysis (DISS error) could lead to a false negative, i.e. concluding that the sexes responded similarly when they responded differently. The sex × treatment interaction, which is statistically significant (P=0.038), indicates the difference in the responses of females and males. Because of this significant interaction, the data from males and females are presented separately (right panel) and post hoc tests of the effect of treatment are presented for each sex. See Figure 2—source data 1 for the data depicted in A and B.
-
Figure 2—source data 1
Source data for Figure 2, showing the response of females and males to a control or experimental treatment.
- https://cdn.elifesciences.org/articles/90623/elife-90623-fig2-data1-v2.xlsx
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Science Forum: Best practices to promote rigor and reproducibility in the era of sex-inclusive research
eLife 12:e90623.
https://doi.org/10.7554/eLife.90623
