The computational nature of memory modification
Figures
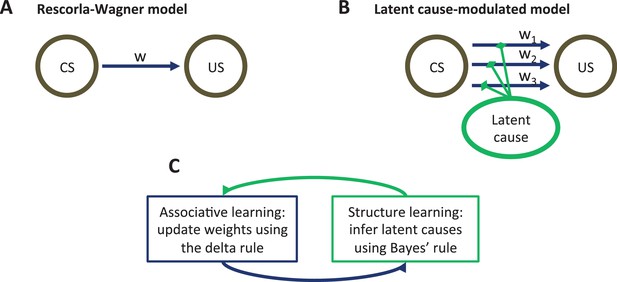
Model schematic.
(A) The associative structure underlying the Rescorla-Wagner model. The associative strength between a conditioned stimulus (CS) and an unconditioned stimulus (US) is encoded by a scalar weight, , that is updated through learning. (B) The associative structure underlying the latent-cause-modulated model. As in the Rescorla-Wagner model, associative strength is encoded by a scalar weight, but in this case there is a collection of such weights, each paired with a different latent cause. The US prediction is a linear combination of weights, modulated by the posterior probability that the corresponding latent cause is active. Alternatively, this model can be understood as consisting of three-way associations between the latent cause, the CS and the US. (C) A high-level schematic of the computations in the latent-cause model. Associative learning, in which the associative weights are updated (using the delta rule) conditional on the latent-cause posterior, alternates with structure learning, in which the posterior is updated (using Bayes’ rule) conditional on the weights.
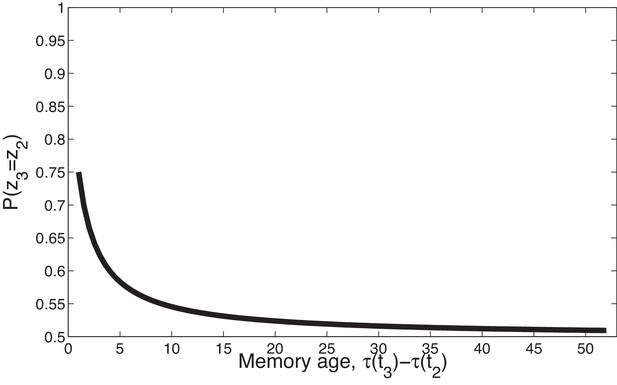
Temporal compression with the power law kernel.
We assume that was generated by cause , two timepoints later was generated by cause , and a variable number of timepoints later was generated by cause . To illustrate the time compression property we have assumed that the probability of a new cause is 0 (i.e., ) so inference at is constrained to one of the previous causes. As the temporal distance between and the time of the previous trial increases, that is, as the memory for recedes into the past, the probability of trial three being generated by either of the two prior latent causes becomes increasingly similar.
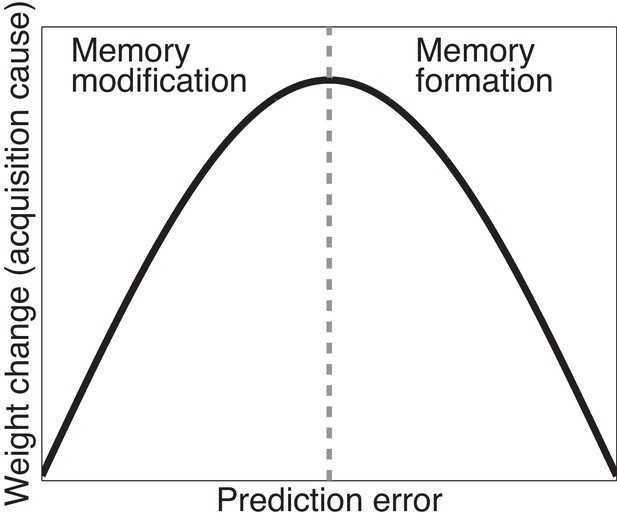
Cartoon of the model’s predictions for fear extinction.
The X-axis represents the size of the prediction error during extinction, and the Y-axis represents the change (after learning) in the weight for US prediction for the ‘acquisition latent cause’ (i.e., the latent cause inferred by the animal during conditioning).
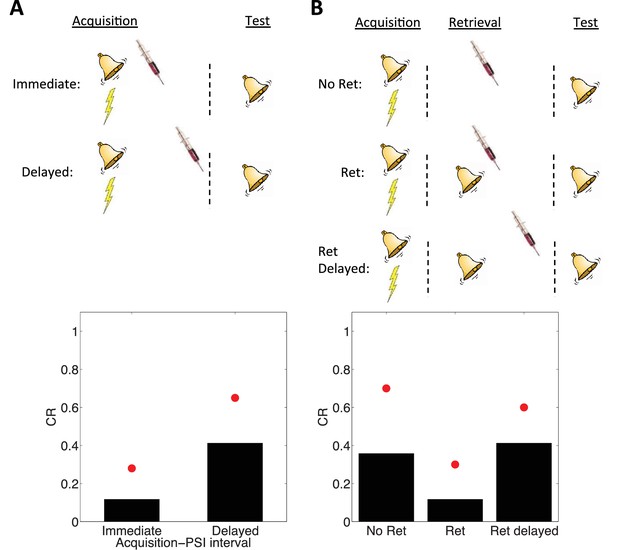
Simulation of post-retrieval memory modification.
Top row shows a schematic of the experimental design (bell represents the tone CS, lightning bolt represents the shock US, syringe represents the injection of a protein synthesis inhibitor), with a conditioning extinction test structure. Bottom row shows model predictions in the test phase. (A) PSIs disrupt a fear memory (measured here through a freezing CR) when delivered immediately after the acquisition phase, but not when delivered after a delay. Red circles show proportion freezing of rats in the study by Schafe and LeDoux (2000). (B) The delayed PSI administration is effective at disrupting the memory following reexposure to the CS (Ret). The effectiveness of this procedure is diminished if the PSI administration is delayed relative to reexposure (Ret delayed). Red circles show proportion freezing of rats in the study by Nader et al. (2000).
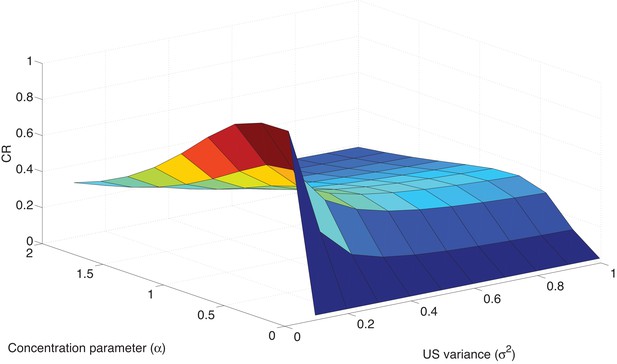
Parameter sensitivity in the Ret condition.
https://doi.org/10.7554/eLife.23763.007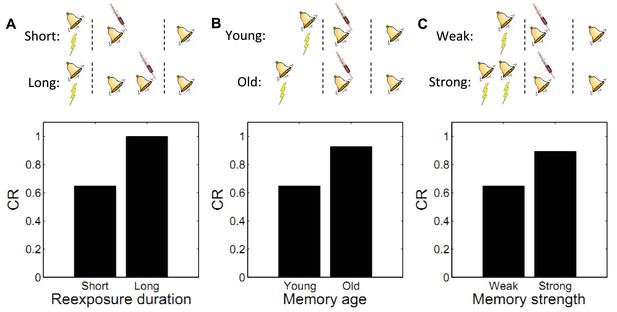
Boundary conditions on memory modification.
Memory updating is attenuated under conditions of (A) more reexposure, (B) older or (C) stronger memories.
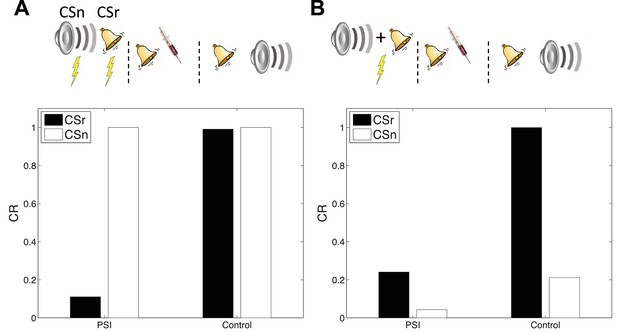
Cue-specificity of amnestic treatment.
(A) Disruption of memory modification by amnestic treatment affects the reactivated cue (CSr) but not the non-reactivated cue (CSn). (B) When trained in compound, reactivating CSr renders CSn vulnerable to disruption of modification.
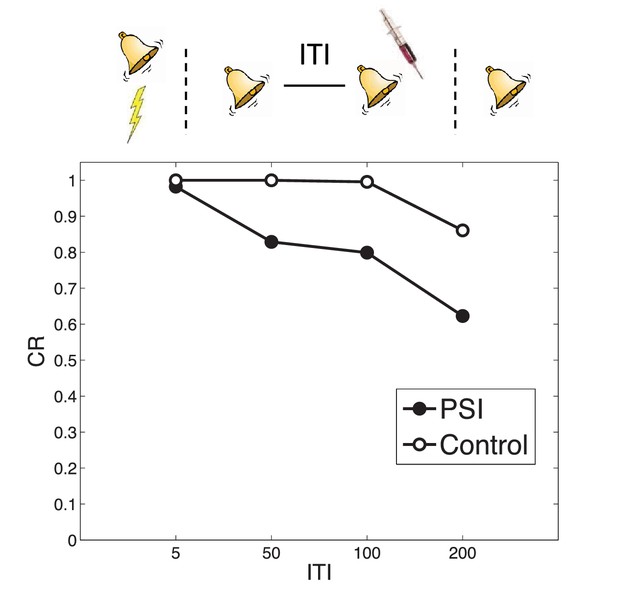
Timing of multiple reexposures.
Lengthening the intertrial interval (ITI) between multiple reexposures increases the simulated effectiveness of PSI administration in attenuating fear at test. The control simulation shows results without PSI administration.
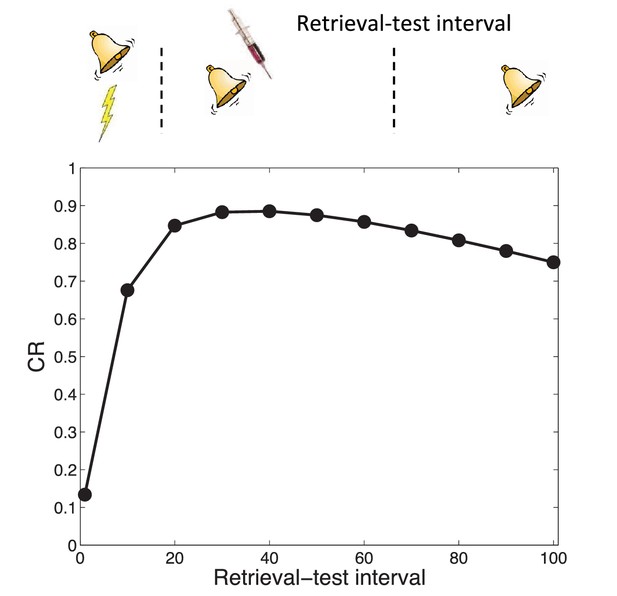
Transience of amnesia.
Lengthening the interval between retrieval and test results in recovery from amnesia.
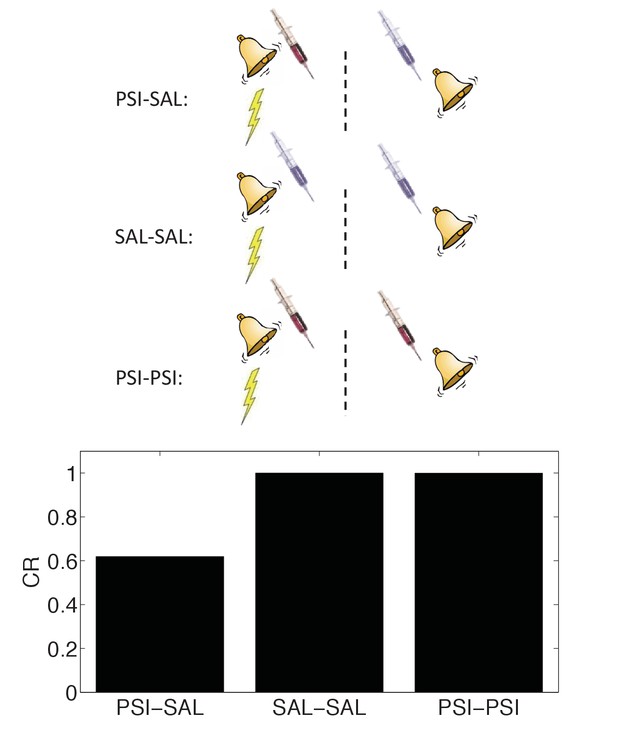
State-dependency of amnesia.
The amnestic affect of PSI administration after conditioning can be reversed by readministering the PSI at the time of test (‘PSI-PSI’). Here ‘SAL’ denotes administration of saline instead of the PSI, indicated by the pale syringe in the schematic.
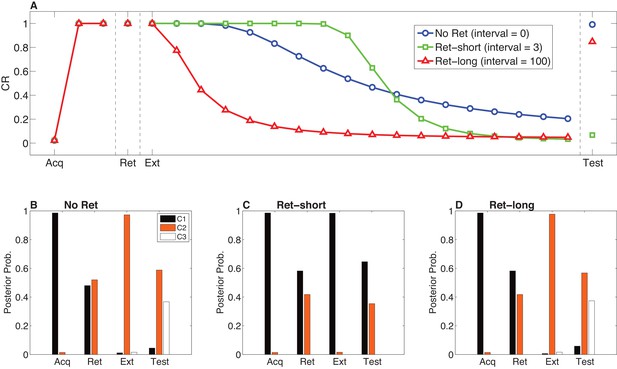
Model predictions for the Monfils-Schiller paradigm.
(A) Simulated conditioned response (CR) during acquisition (Acq; 3 CS-US pairs), retrieval (Ret; 1 CS presentation 24 hr after acquisition, followed by no interval, a short interval, or a long interval before the next phase), extinction (Ext; CS-alone presentations) and a test phase 24 hr later. Three conditions are shown: No-Ret (no interval between retrieval and extinction; the ‘Ret’ trial depicted here is the first trial of extinction), Ret-short (retrieval with a short post-retrieval interval), and Ret-long (retrieval with a long post-retrieval interval). (B–D) The posterior probability distribution over latent causes (denoted C1, C2 and C3) in each condition. Probabilities for only the top three highest-probability causes are shown.
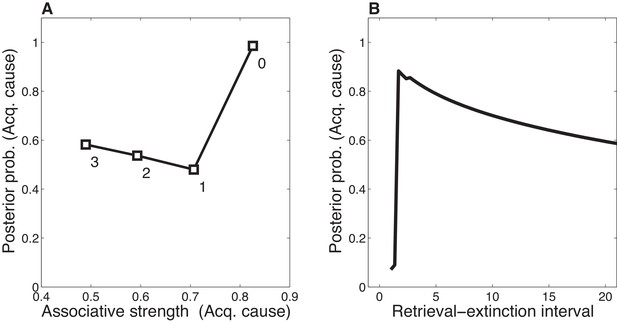
Dynamics of associative and structure learning during the retrieval-extinction interval in the Monfils-Schiller paradigm.
(A) The X-axis represents the associative weight corresponding to the acquisition latent cause. The Y-axis represents the posterior probability that the acquisition latent cause is active for the retrieval trial. Each numbered square indicates a particular iteration during the retrieval-extinction interval, with '0' indicating the last trial of acquisition. Initially, the prediction error causes the posterior to favor a new latent cause rather than the old acquisition cause, however, over the course of three iterations, incremental reductions in the associative weight pull the posterior probability higher by making the retrieval trial more likely under the acquisition cause. (B) As the retrieval-extinction interval grows longer, the probability of assigning the first extinction trial to the acquisition cause changes non-monotonically. Two non-reinforced trials very close in time are likely to come from a new latent cause, thus the posterior probability of the acquisition cause generating these trials starts low. It peaks at a larger retrieval-extinction interval; as this interval increases, the acquisition cause’s associative strength is incrementally reduced, thereby making the extinction trials more likely under the acquisition cause. The curve then gradually diminishes due to the time-sensitive prior that causes temporally separated events to be more likely to be generated by different causes (Equation 3). Each EM iteration takes a single timestep, and at least 1 EM iteration is always performed, up to a maximum of 3, depending on the intertrial interval.
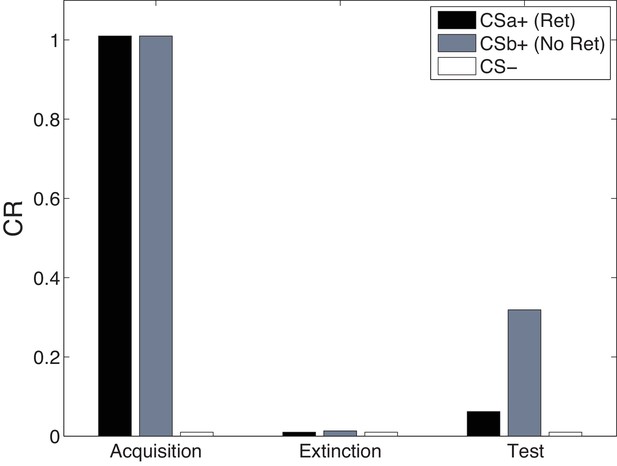
Cue-specificity in the Monfils-Schiller paradigm.
Model simulations of the within-subjects design reported by Schiller et al. (2010), in which two CSs (CSa and CSb) were individually paired with shock (CS was never paired with a shock), but only one (CSa) was reexposed in a ‘retrieval’ trial prior to extinction. Fear recovery is attenuated for the reexposed CS.
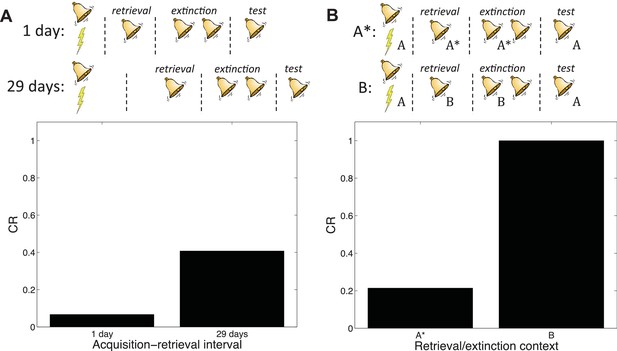
Boundary conditions in the Monfils-Schiller paradigm.
(A) A short acquisition-retrieval interval is more effective at attenuating spontaneous recovery of fear at test than a long acquisition-retrieval interval. (B) A retrieval/extinction context (A*) that is similar to the acquisition context (A) leads to attenuated renewal of fear when tested in A, whereas a very dissimilar context (B) leads to renewal.
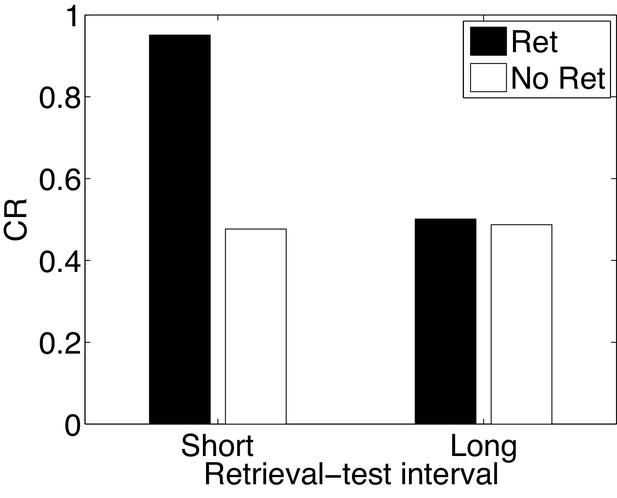
Paradoxical enhancement of memory.
A weak conditioned response is first acquired using a low-intensity US (in order to prevent a ceiling effect). The graph shows the conditioned response at test following a retrieval cue (Ret) or no retrieval cue (No Ret) at short and long retrieval-test intervals.





