Judgments of agency are affected by sensory noise without recruiting metacognitive processing
- Faculty of Life Sciences, Department of Psychology, Humboldt-Universität zu Berlin, Germany
- Bernstein Center for Computational Neuroscience Berlin, Germany
- Berlin School of Mind and Brain, Humboldt-Universität zu Berlin, Germany
- Gonda Multidisciplinary Brain Research Center, Bar-Ilan University, Israel
Figures
Figure 1
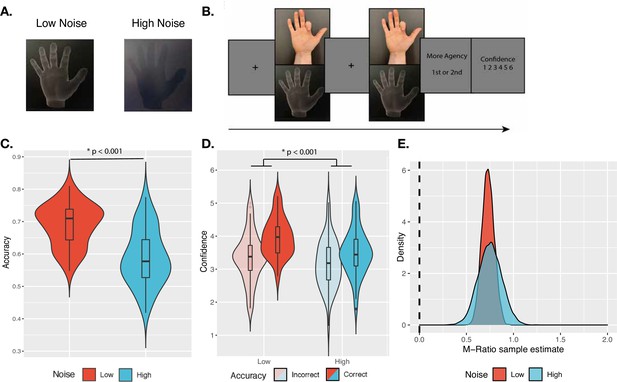
Confidence task.
(A) Sensory noise conditions. Sensory noise was manipulated by changing the illumination, with high sensory noise captured by low contrast, dark illumination, and low sensory noise captured by high contrast, bright illumination. (B) Experimental paradigm. Cued by the offset of the fixation cross, participants made two consecutive finger movements on each trial, with their hand out of sight. On the screen, participants saw either a virtual hand moving in synchrony with their own, or with an additional temporal delay. Participants first discriminated which movement they felt more agency over, and then rated their confidence in their own response. (C) Discrimination accuracy. In line with the intended effect of the sensory noise manipulation, accuracy was significantly higher for low- vs. high-noise conditions. (D) Mean confidence ratings. We found a significant interaction effect between Response Accuracy and Noise on Confidence. Violin plots capture the kernel probability density and boxplots show the median, interquartile range (IQR) with hinges showing the first and third quartiles, and vertical whiskers stretching to most extreme data point within 1.5*IQR from the hinges. Outliers are plotted as black or gray dots. (E) M-Ratio Estimates. Metacognitive efficiency for each noise level, estimated using the HMetad′ toolbox. The dashed vertical line indicates chance-level metacognitive efficiency.
Figure 2
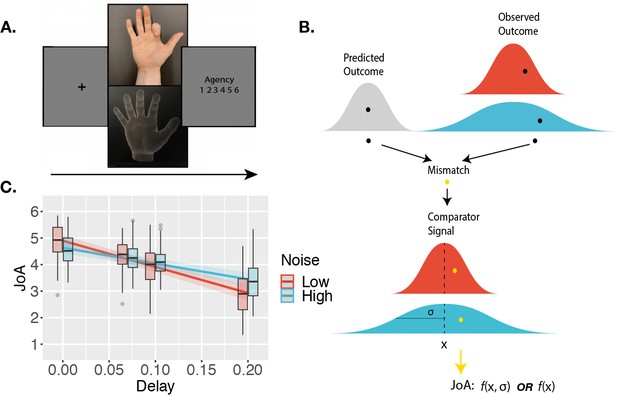
Agency-rating task.
(A) Experimental paradigm. Cued by the offset of the fixation cross, participants made one finger movement on each trial, with their hand out of sight. On the screen, participants saw either a virtual hand moving in synchrony with their own, or with an additional delay/temporal lag. Participants then made a judgment of the degree of agency they experienced. (B) Sketch of noise dependency prediction. By decreasing the illumination of the scene, the high-noise condition adds sensory noise to the observed outcome, and hence to the comparator signal, computed as the mismatch between predicted and observed outcomes. This environmental noise, independent of the delay, leads to a noisier mapping between the actual delay in the environment and the perceived internal signal. According to the comparator model, this internal delay signal is then compared to the representation of the predicted outcome, leading to the internal comparator signal. The internal comparator signal is represented as the bottom-most red (low uncertainty) and blue (high uncertainty) probability distributions. Points reflect the perceived signals on single trials. If the JoA is a readout of the comparator signal on each trial, though the variance would increase with noise, the mean JoA will not depend on noise, but will reflect the mean of the comparator signal distribution. Alternatively, if JoAs monitor the noisiness of the comparator signal, mean JoA will depend on noise. In other words, JoAs would be a function not only of a noisy signal (x), but of the noisy signal and the noise itself (σ). (C) Interaction effect result. Predicted JoA across delays and noise conditions from linear mixed-effects model results. 95% confidence intervals shown. Boxplots reflect subjectwise mean JoAs per noise level and delay. They show the median, interquartile range (IQR) with hinges showing the first and third quartiles, and vertical whiskers stretching to most extreme data point within 1.5*IQR from the hinges. Outliers are plotted as gray dots.
Figure 3
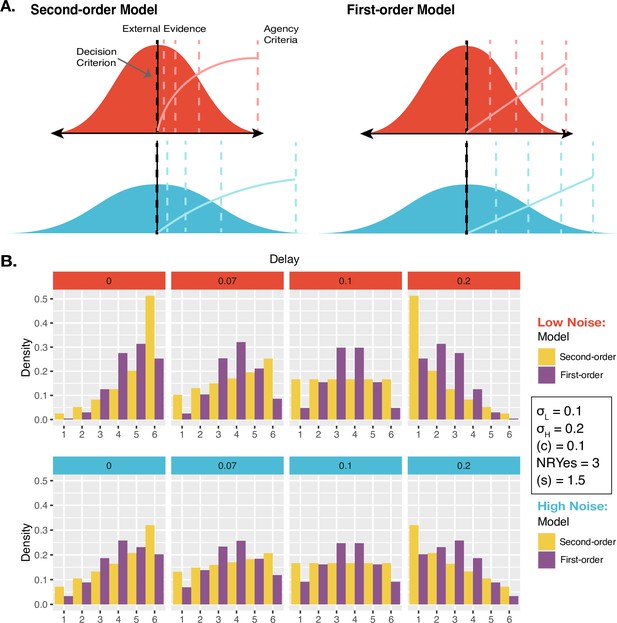
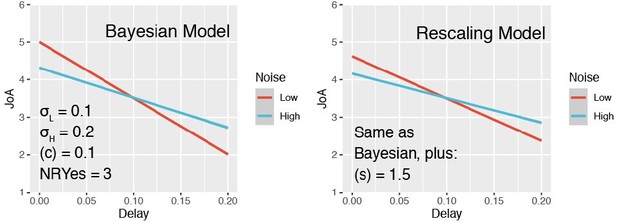
Models and Predictions.
(A) Two models of JoAs. In the Second-order model of agency, JoA reflects the posterior probability of the detection decision being correct, given the choice and internal evidence. The Gaussian distributions are probability distributions of the internal comparator signal. The dashed colored lines indicate the criteria, or the thresholds on the internal signal axis that delineate the different JoA values. These are spaced linearly in probability space, so their positions on the internal signal space change with noise level. The solid colored lines show the expected JoAs as a function of internal signal strength. In the First-order model of agency, JoA reflects a first-order estimate of delay compared to the criterion, not based on noise. However, the criteria are spread evenly across the range of signals within each noise level, such that they interact with noise level only due to a rescaling of ratings. The solid colored lines show the predicted JoA as a function of internal signal strength. Note that this function is linear but still interacts with noise, due to the rescaling. (B) Example model predictions. To illustrate the predictions of each of the models, we chose representative parameter values to run simulations. These values fall within the range of the values resulting from the model fits to participants’ data. Predicted distributions of JoAs per delay and noise condition are shown as densities.
Figure 4
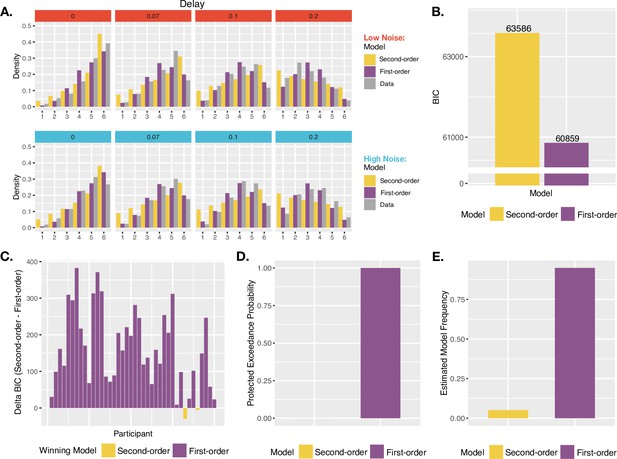
Agency model fits and results.
(A) Model fits. Simulated probability of each JoA for a given delay and noise level, given best fitting parameters from the MLE analysis for Second-order and First-order models. These are portrayed as densities across the JoAs. Data distributions are shown in shaded gray, also portrayed as densities across discrete ratings. (B) Group BIC Results. BIC comparison between Second-order and First-order models on pooled JoA data. (C) Subject-wise BIC Results. Difference in BIC (Second-order - First-order) for each participant, with negative values indicating that the Second-order model fit better, and positive values indicating that the First-order model fit better. (D) Protected Exceedance Probabilities. Protected exceedance probabilities of the Second-order and First-order models. (E) Estimated Model Frequencies. Predicted model frequencies estimated from the exceedance probability analysis.
Figure 5
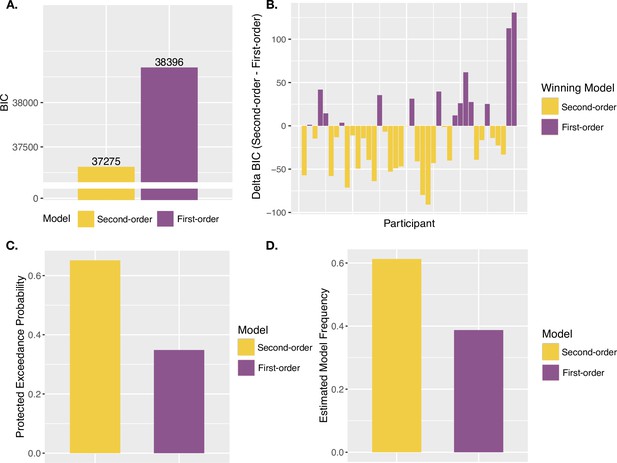
Confidence model results.
(A) Group BIC Results. BIC comparison between the Second-order and First-order models on pooled confidence rating data. (B) Subject-wise BIC Results. Difference in BIC (Second-order - First-order) for each participant, with negative values indicating that the Second-order model fit better, and positive values indicating that the First-order model fit better. (C) Protected Exceedance Probabilities. Protected exceedance probabilities of the Second-order and First-order models. (D) Estimated Model Frequencies. Predicted model frequencies estimated from the exceedance probability analysis.
Figure 6
Function of internal evidence as estimated by each of the models tested.
Agency as a function of evidence strength computations in each model. In the Second-order model this function of internal evidence reflects confidence based on the posterior probability of having given a correct response, given internal signal and choice. In the First-order model this is based on the perceived distance between signal and criterion.
Appendix 1—figure 1
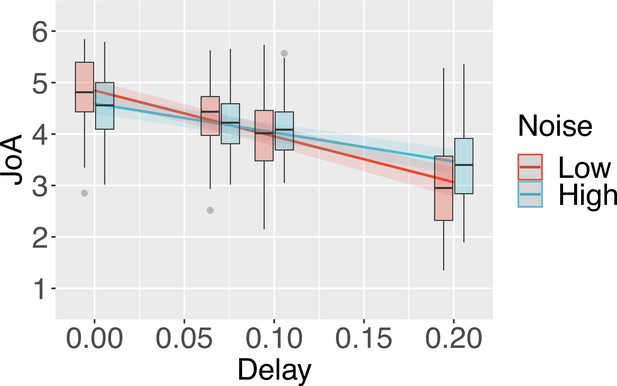
Interaction effect result with all participants.
Predicted JoA across delays and noise conditions from linear mixed-effects model results. 95% confidence intervals shown. Boxplots reflect subjectwise mean JoAs per noise level and delay. They show the median, interquartile range (IQR) with hinges showing the first and third quartiles, and vertical whiskers stretching to most extreme data point within 1.5*IQR from the hinges. Outliers are plotted as gray dots. The model was run on data from all 47 participants.
Appendix 3—figure 1
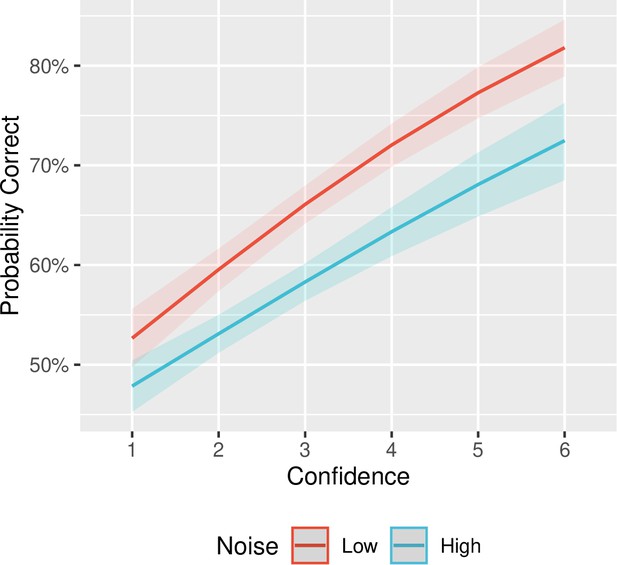
Logistic regression results.
Metacognitive sensitivity quantified with predicted probability correct across confidence ratings and noise conditions from mixed logistic regression model results. We found a significant interaction between noise and confidence, with a smaller slope of confidence across accuracy under high noise. 95% confidence intervals shown.
Appendix 4—figure 1
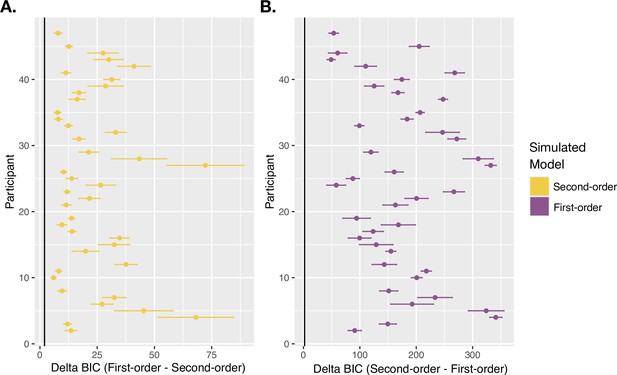
Model recovery results.
BIC differences between the Second-order and First-order models, with positive values favoring the simulated model, fit to simulated datasets using all participants’ winning parameter sets for each model. (A) BIC comparison results from datasets simulated with the Second-order model and the winning parameters for the Second-order model for each participant. (B) BIC comparison results from datasets simulated with the First-order model and the winning parameters for the First-order model for each participant. Points reflect the mean BIC difference across 20 repetitions of each parameter set, and error bars show the standard error. The black vertical line indicates the minimum BIC difference of 2 required for the correct model to be considered the better fitting model.
Appendix 5—figure 1
BIC results from confidence Task.
BIC comparison between the Second-order and First-order models on pooled confidence rating data, using calculated decision criteria and difference between noise conditions.
Author response image 1
Tables
Table 1
Syntax for the linear mixed-effects models used.
| Task | Hypothesis | Model formula |
|---|---|---|
| Confidence Task | Sensory noise influences response accuracy | logit(Response Accuracy)~ Noise + (1 | Participant) |
| Confidence Task | Sensory noise influences confidence following correct decisions | Confidence~ Response + Response Accuracy*Noise + (1 | Participant) |
| Agency Rating Task | Sensory noise influences the effect of delay on JoA | JoA ~ Delay*Noise + (Delay:Noise | Participant) |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Judgments of agency are affected by sensory noise without recruiting metacognitive processing
eLife 11:e72356.
https://doi.org/10.7554/eLife.72356
