Crowding-induced phase separation of nuclear transport receptors in FG nucleoporin assemblies
- Department of Physics and Astronomy, University College London, United Kingdom
- Institute for the Physics of Living Systems, University College London, United Kingdom
- London Centre for Nanotechnology, University College London, United Kingdom
Figures
Figure 1 with 2 supplements
Setting the polymer-particle cohesion strengths through comparison of density functional theory (DFT) results with experimental binding isotherms for the cases of NTF2 (left) and Importin- (Imp-β) (right) binding to an Nsp1 film (Zahn et al., 2016) (top).
Concomitant film thicknesses as found in DFT and experiment (bottom). The experimental Nsp1 surface attachment densities were 4.9 pmol/cm2 and 5.1 pmol/cm2 for NTF2 and Imp-β, respectively. The parametrised cohesion strengths and correspond to the modelled NTF2 and Imp-β particles, respectively. Filled bands (in all four panels) denote a tolerance of ±0.1 in the polymer-particle cohesion strengths. The thicknesses of the filled bands for the bottom two panels are similar to the thickness of the line connecting DFT data points (blue and orange).
-
Figure 1—source code 1
Simulation parameters for the classical density functional theory code.
- https://cdn.elifesciences.org/articles/72627/elife-72627-fig1-code1-v2.zip
Figure 1—figure supplement 1
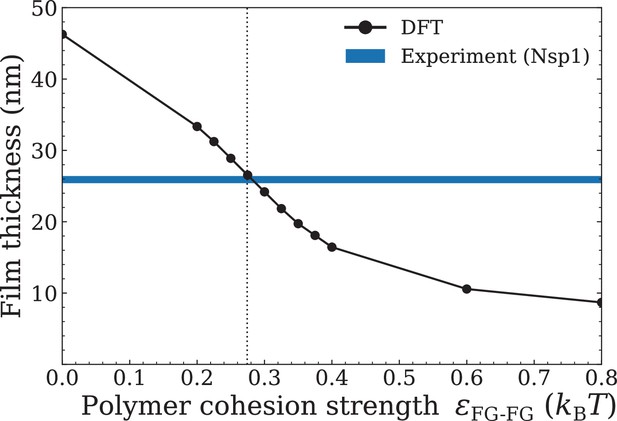
Parameterising the polymer cohesion strength .
Setting the polymer-polymer cohesion parameter through comparison of film thicknesses as calculated from density functional theory (DFT), i.e., the height including 95% of polymer density, with the film thickness of an Nsp1 film assembly as derived from experiment (25.9 ± 0.5 nm) (Zahn et al., 2016). The grafting density of Nsp1 to the flat surface in DFT was set so as to best match the density used in experiments (4.9 pmol/cm2 ≈3.3 polymers/100 nm2). The vertical dotted line corresponds to the interpolated for which the DFT best matches the experimental thickness.
Figure 1—figure supplement 2
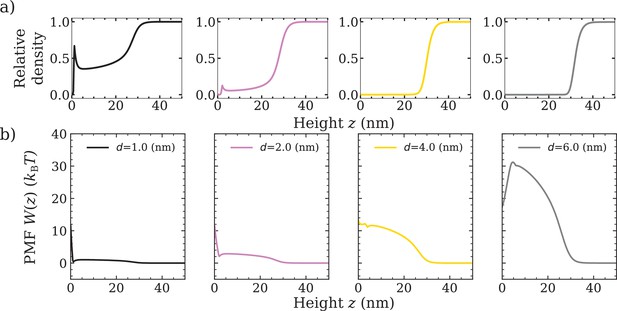
Inert particles of growing size do not penetrate the polymer film.
Inert particles of growing size do not penetrate the polymer film. Quantification of entry (to the Nsp1 film) barriers for non-cohesive particles with varying diameters . (a) Relative density (normalised to the bulk value occurring at nm) of non-cohesive particles with diameters nm (black), nm (pink), nm (gold), nm (grey) as calculated in classical density functional theory. (b) Potential of mean force as a function of the height above the flat surface . The concentration of the particles in the solution is 10.0 for all panels. The polymer-polymer cohesion strength is , as set through comparison with an experimental Nsp1 film.
Figure 2 with 1 supplement
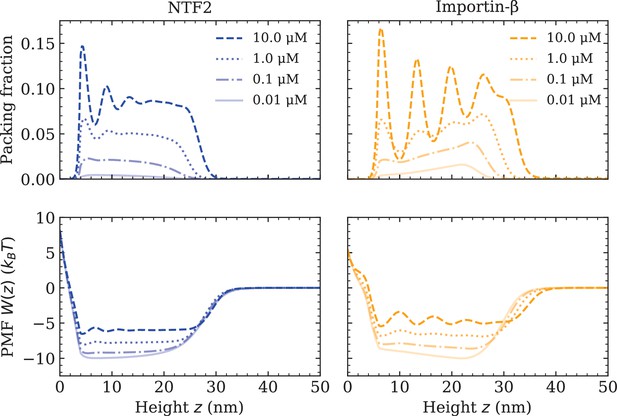
Increasing nuclear transport receptor (NTR) bulk concentration increases packing and filling up of the potential well within the Nsp1 film, for systems containing one type of NTR only.
Equilibrium density functional theory packing fractions , where is the one-dimensional number density and is the particle diameter, as a function of the height above the flat surface for NTF2 (left) and Importin- (right), at various concentrations (top). Accompanying potentials of mean force (bottom), for the same systems as on the top row.
Figure 2—figure supplement 1
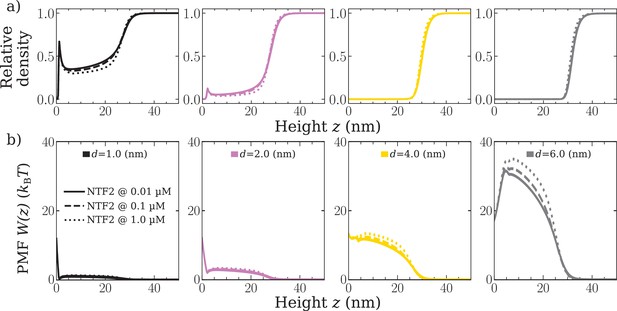
The presence of NTF2 enhances the entry barrier for inert particles.
Increasing presence of NTF2 increases the entry barrier for inert/non-cohesive particles of varying size. (a) Relative density (normalised to the bulk value occurring at z ≥40 nm) of non-cohesive particles with diameters = 1.0 nm (black), = 2.0 nm (pink), = 4.0 nm (gold), = 6.0 nm (grey) for increasing bulk concentrations of NTF2, as calculated in classical density functional theory. (b) Potential of mean force as a function of the height above the flat surface . The concentration of the non-cohesive particles in the solution is 10.0 µM for all panels. The polymer-polymer cohesion strength is and the NTF2-polymer cohesion strength is , as set through comparisons with experiments.
Figure 3 with 2 supplements
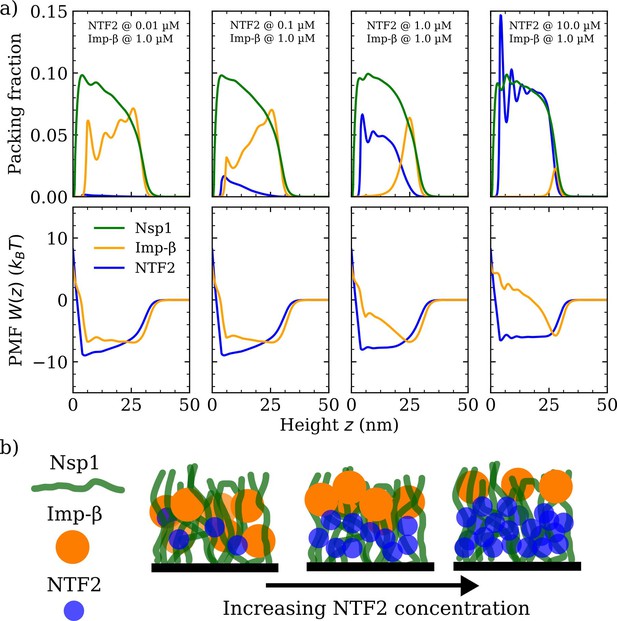
Phase separation in a ternary phenylalanine-glycine nucleoporins (FG Nup)-nuclear transport receptor polymer film assembly.
(a) Density functional theory packing fractions and accompanying potentials of mean force (PMFs) for Nsp1 polymer films in the presence of NTF2 and Importin- (Imp-). The concentration (in solution) of NTF2 is increased from 0.01 to 10.0 µM (left to right panels), whilst the concentration of Imp- is fixed at 1.0 µM. The cohesion strengths used here are for the Nsp1-Nsp1, Nsp1-NTF2, and Nsp1 - Imp- interactions, respectively. (b) Cartoon visualisation of the data from (a) depicting the increasing concentration of NTF2 pushing Imp- to the top of the Nsp1 layer, also resulting in significant expulsion of Imp- from the film into the bulk.
-
Figure 3—source code 1
Simulation parameters for the classical density functional theory code.
- https://cdn.elifesciences.org/articles/72627/elife-72627-fig3-code1-v2.zip
Figure 3—figure supplement 1
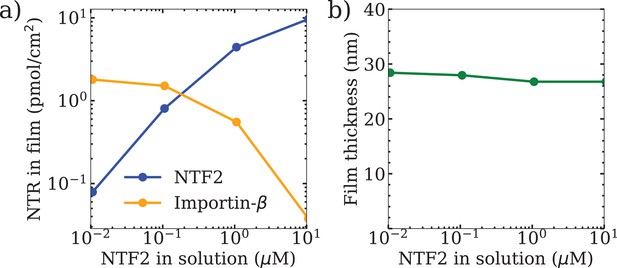
Nuclear transport receptor (NTR) binding isotherms and Nsp1 film thicknesses as a function of NTF2 concentration in solution, in the presence of 1 µM Importin- (Imp-β).
NTR binding isotherms and Nsp1 film thicknesses as a function of NTF2 concentration in solution, in the presence of 1 µM Imp-. (a) Binding isotherms as predicted from the classical density functional theory (DFT) model for NTF2 and Imp-. (b) Concomitant film thickness of the phenylalanine-glycine nucleoporins (FG Nup) (Nsp1) layer as found in DFT. The cohesion strengths used here are for the Nsp1-Nsp1, Nsp1-NTF2, and Nsp1 - Imp- interactions, respectively. In each plot the concentration of Imp- in solution remained – approximately – fixed at 1 µM.
Figure 3—figure supplement 2
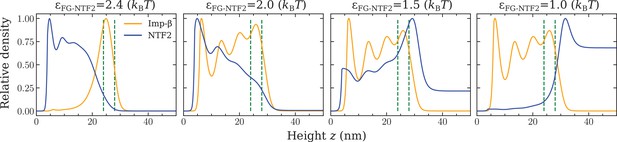
Varying the cohesion between NTF2 molecules and phenylalanine-glycine nucleoporins (FG Nups) modulates the distribution of Importin- (Imp-β).
Decreasing the NTF2-FG Nup cohesion strength () facilitates the further inclusion of modelled Imp-. Relative density, normalised to the maximum density in the system, as a function of the height above the anchoring surface. The two green dashed lines are the lower (24 nm) and upper (28 nm) bounds of the FG Nup film thickness as found through comparison with experiments (Zahn et al., 2016). The bulk concentrations of each NTR is 1 µM and the polymer-polymer cohesion strength is in all plots.
Figure 4 with 1 supplement
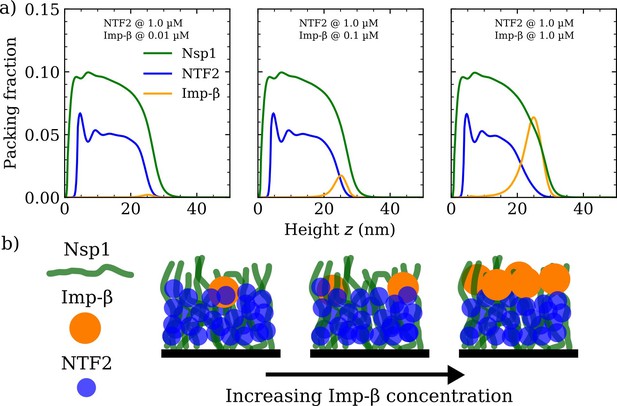
Increasing Importin- (Imp-) concentration negligibly affects NTF2 in the Nsp1 film.
(a) Density functional theory packing fractions against the height above the flat surface for Nsp1, NTF2, and Imp-. The concentration of Imp- is increased from 0.01 to 10 µM (left to right panels) whilst the NTF2 concentration remains fixed at 1.0 µM. The last panel (furthest to the right) is the same as the second last panel in Figure 3a. (b) Cartoon illustration visualising the data in (a) depicting the undetectable change in the packing/morphology of the NTF2 in the presence of increasing Imp- molecules.
Figure 4—figure supplement 1
Nuclear transport receptor (NTR) binding isotherms and Nsp1 film thicknesses as a function of Importin- (Imp-β) concentration in solution.
NTR binding isotherms and Nsp1 film thicknesses as a function of Imp- concentration in solution. (a) Binding isotherms as predicted from the classical density functional (DFT) model for NTF2 and Imp-. (b) Concomitant film thickness of the phenylalanine-glycine nucleoporins (FG Nup) (Nsp1) layer as found in DFT. The cohesion strengths used here are for the Nsp1-Nsp1, Nsp1-NTF2, and Nsp1 - Imp- interactions, respectively. In each plot the concentration of NTF2 in solution remained – approximately – fixed at 1 µM.
Figure 5 with 2 supplements
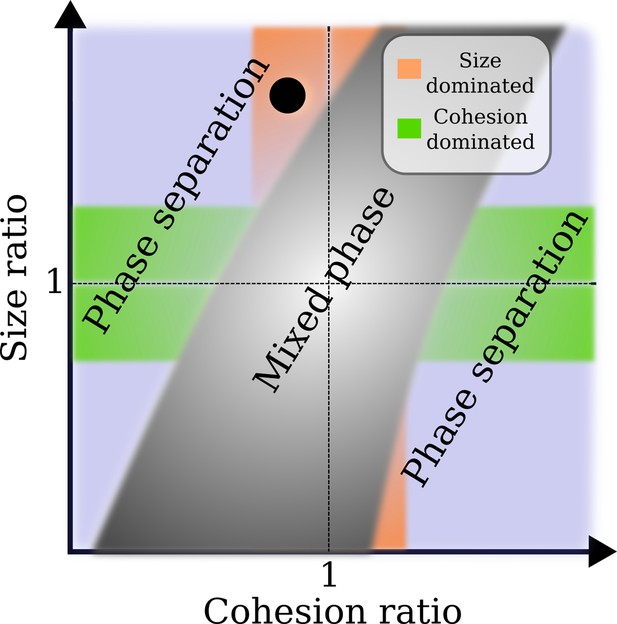
Approximate phase diagram for the crowding of two different types of nuclear transport receptor (NTR)-like particles in an Nsp1 film, based on simulations for particle sizes between 2 and 6 nm, and their affinities (cf., and ) to Nsp1 between ∼0 and ∼10 .
Plotted as a linear function of both the size ratio and cohesion (or affinity) ratio, the phase diagram shows a mixed phase (grey), where the density profiles of the NTR-like particles in the Nsp1 film have substantial overlap, and a phase separated state (not grey), where the profiles of the NTRs are sufficiently separated resulting in an interface. In the orange region the cohesion ratio of the NTRs is close to unity whereas the size ratio is far from unity, indicating that the phase separation results from the difference in NTR size. The green region is the exact opposite of the orange region: the cohesion ratio of the NTRs is far from unity whereas the size ratio is close to unity, indicating that the phase separation results from the difference in NTR cohesion. The blue region encompasses the cases where both the size and cohesion ratios are far from unity. The black circle represents the phase separation of modelled Importin- (Imp-β) and NTF2 ( and ) as found in this work.
Figure 5—figure supplement 1
Relative density plots for selected points in the phase diagram.
Relative density plots (a-i) for selected points in the phase diagram (see Figure 5). Vertical axis is the relative density, i.e., density divided by the maximum density in the system, for two nuclear transport receptor (NTR)-like particles (1 and 2) interacting with a polymer film assembly, as a function of height above the anchoring surface, for different particle sizes (in units of nm) and cohesion strengths (in units of ) between the individual NTR-like particle and the phenylalanine-glycine nucleoporins (FG Nups), as found in classical density functional theory (a) (b) (c) (d) (e) (f) (g) (h) (i) . The two green dashed lines are the lower (24 nm) and upper (28 nm) bounds of the FG Nup film thickness as found through comparison with experiments (Zahn et al., 2016). The bulk concentrations of each particle is 1 µM and the polymer-polymer cohesion strength is in all plots.
Figure 5—figure supplement 2
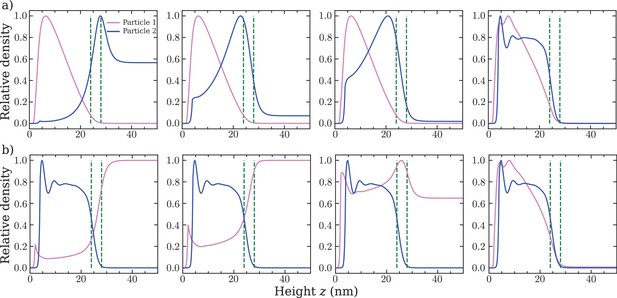
Modelled nuclear transport receptor (NTRs) particles of diameters 2 nm and 4 nm hardly affect each other’s distribution within the film.
Modelled NTRs of diameters 2 nm (pink) and 4 nm (blue) hardly affect each other’s distribution within the film. (a) Relative density, normalised to the maximum density in the system, of two NTR-like particles as a function of the height above the anchoring surface, for decreasing (left to right) NTR-phenylalanine-glycine nucleoporin (FG Nup) cohesion strength ratio ( with ). (b) Same as (a) but for increasing (left to right) NTR-FG Nup cohesion strength ratio ( with ). In both (a) and (b) the two green dashed lines are the lower (24 nm) and upper (28 nm) bounds of the FG Nup film thickness as found through comparison with experiments (Zahn et al., 2016). The bulk concentrations of each NTR-like particle is 1 µM and the polymer-polymer cohesion strength is (equivalent to in the Computational methods section) in all plots.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Crowding-induced phase separation of nuclear transport receptors in FG nucleoporin assemblies
eLife 11:e72627.
https://doi.org/10.7554/eLife.72627
