Geometry and dynamics of representations in a precisely balanced memory network related to olfactory cortex
Figures
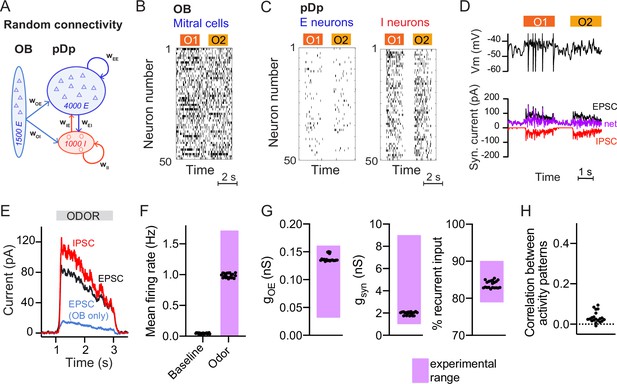
Spiking network model of pDp.
(A) Schematic of pDpsim. OB, olfactory bulb; E, excitatory; I, inhibitory neurons. (B) Spike raster of a random subset of 50 mitral cells in the OB representing 2 odors (O1 and O2). During odor stimulation, firing rates of 10% of mitral cells were increased and firing rates of 5% of mitral cells were decreased (baseline rate, 6 Hz). (C) Spike raster of random subsets of 50 E and I neurons in response to 2 odors. (D) Representative membrane potential trace (top) and excitatory (EPSC, black) and inhibitory (IPSC, red) currents (bottom) in one excitatory neuron in response to two odors. Purple trace shows net current (EPSC + IPSC). (E) Odor-evoked inhibitory (red) and excitatory (black and blue) currents as measured in a hypothetical voltage clamp experiment (conductance multiplied by 70 mV, the absolute difference between holding potential and reversal potential; Rupprecht and Friedrich, 2018). Representative example of one network, averaged across neurons and odors. (F–H) Measured values of the observables used to match pDpsim to experimental data. Each dot represents one network (average over 10 odors); n = 20 networks. Pink shading shows the experimentally observed range of values. (F) Baseline and odor-evoked population firing rate. (G) Left: gOE is the synaptic conductance in E neurons contributed by afferents from the OB during odor stimulation. Middle: gsyn is the total odor-evoked synaptic conductance. Right: % recurrent input quantifies the percentage of E input contributed by recurrent connections during odor stimulation. (H) Correlation coefficient between odor-evoked activity patterns in pDpsim. The dotted line indicates the mean correlation between odor patterns in the OB.
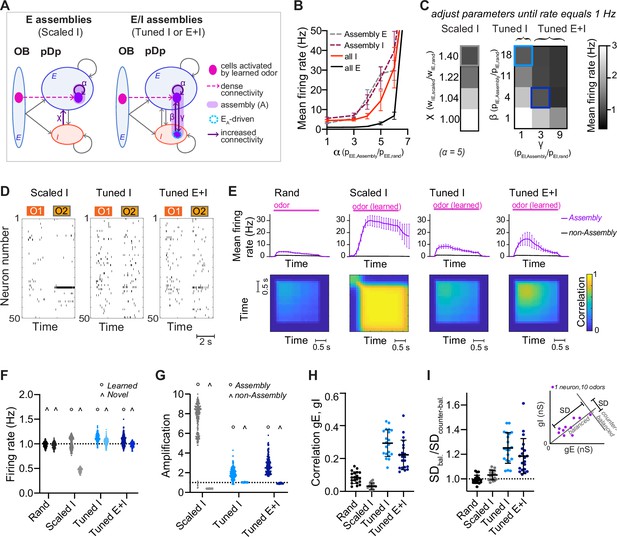
Networks with neuronal assemblies (memories).
(A) Schematic of assemblies. Each assembly contains the 100 E neurons that are most densely connected to the mitral cells activated by a given odor. Connection probability between these E neurons is increased by a factor α. In Scaled I networks, weights of all I-to-E synapses are increased by a factor χ. In Tuned networks, the 25 I neurons that are most densely connected to the 100 E neurons are included in each assembly. In Tuned I networks, the probability of I-to-E connections within the assembly is increased by a factor β. In Tuned E+I networks, probabilities of I-to-E and E-to-I connectivity within the assembly are increased by factors β and γ, respectively. n = 20 networks with 15 assemblies each were simulated for each group. (B) Firing rates averaged over all E or I neurons (full lines) and over all assembly neurons (dashed lines) as a function of α (mean ± SD across 20 networks). (C) Mean E neuron firing rates of Scaled (left) and Tuned (right) networks in response to learned odors as a function of connection strength and probability, respectively. Squares depict parameters used in following figures unless stated otherwise. (D) Spike raster plots showing responses of 50 E neurons to 2 odors (O1: novel odor; O2: learned odor) in a Scaled I and the corresponding Tuned networks (same neurons and odors in the corresponding rand network are shown in Figure 1C). (E) Top: Mean firing rates in response to learned odors as a function of time, averaged across assembly or non-assembly neurons. Bottom: Mean correlation between activity patterns evoked by a learned odor at different time points during odor presentation. Correlation coefficients were calculated between pairs of activity vectors composed of the mean firing rates of E neurons in 100 ms time bins. Activity vectors were taken from the same or different trials, except for the diagonal, where only patterns from different trials were considered. The pink bar indicates odor presentation. (F) Mean firing rate in response to learned odors or novel odors. Each data point represents one network–odor pair (n = 20 networks, 10 odors). (G) Amplification within and outside assemblies, calculated as the ratio between the mean firing rates in response to learned odors averaged over the same populations of neurons in a given structured network (Scaled I, Tuned I, or Tuned E+I) and the corresponding rand network. Each data point represents one network–odor pair. (H) Quantification of co-tuning by the correlation between time-averaged E and I conductances in response to different odors, average across neurons. Each data point corresponds to one network (n = 20). Mean ± SD. (I) Quantification of co-tuning by the ratio of dispersion of joint conductances along balanced and counter-balanced axes (inset; Methods; n = 20 networks).
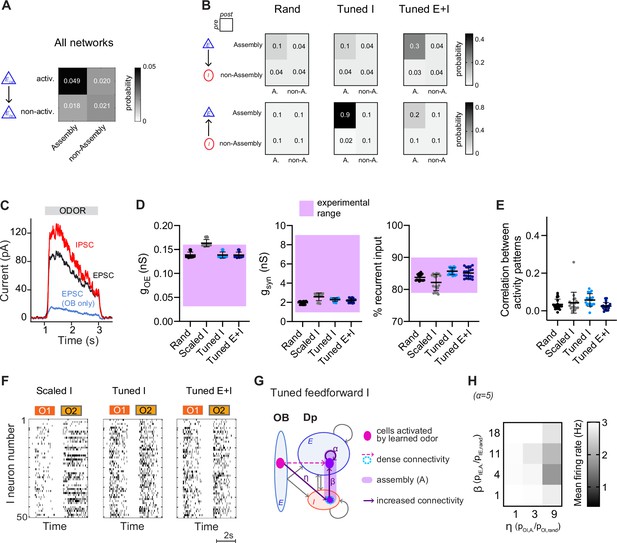
Structured networks reproduce key features of pDp.
(A) Connection probability between activated (activ.) or non-activated (non-activ.) mitral cells and assembly or non-assembly neurons. (B) Connection probability between classes of E and I neurons in a rand, a Tuned I, and a Tuned E+I network. (C) EPSCs and IPSCs in a Tuned I network as observed in a hypothetical voltage clamp recording, averaged across neurons and odors. An equivalent plot for a rand network is shown in Figure 1E. (D, E) Values of observables for rand networks (same as Figure 1G, H) and different structured networks (Scaled I, Tuned I, and Tuned E+I). (F) Spike raster plots showing responses of 50 I neurons to 2 odors (O1: novel odor; O2: learned odor) in a Scaled I and the corresponding Tuned networks (same neurons and odors in the corresponding rand network are shown in Figure 1C). (G) Network with increased connectivity between the E assembly neurons (α = 5) and the 25 I neurons that are most densely connected to the mitral cells activated by a given odor. (H) Mean firing rate of the network in (E) in response to learned odors as a function of connection probability. Activity could not be stabilized efficiently by selecting I neurons based on their afferent connectivity.
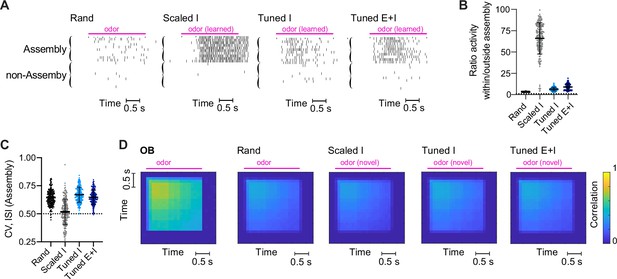
Structured networks: additional results.
(A) Raster plots showing responses of assembly or non-assembly neurons to a learned odor. (B) Ratio of the average firing rate of (pseudo-)assembly neurons to non-assembly neurons in response to learned odors. Each data point represents one network-odor pair (n = 20 networks, 10 odors). Mean ± SD. (C) Coefficients of variation of the inter-spike interval (ISI) in assembly neurons. (D) Correlation between activity patterns across E neurons evoked by the same novel odor in different trials as a function of time. Pink bar indicates odor presentation. Note that correlations in response to novel odors are similar across networks and different from responses to learned odors in Scaled and Tuned networks (Figure 2E).
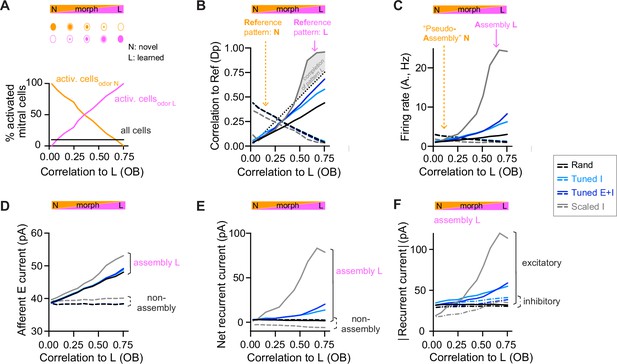
Changes of output activity to gradual modifications of inputs.
(A) Morphing of a novel odor N into a learned odor L. Morphed odors were generated by gradually changing the fractions of activated mitral cells defining odors N or L. The x-axis indicates the similarity of a morphed odor to odor L, here quantified by the correlation between the olfactory bulb (OB) activity patterns representing the morphed and the learned odors (same x-axis in all panels). (B) Pearson correlation between activity patterns evoked by a morphed odor and a learned odor in pDpsim as a function of the corresponding correlations in the OB (full line). The dashed line shows the correlation to the novel odor instead of the learned odor. A signature of pattern completion is a steep increase in the correlation between activity patterns representing a morphed and a learned odor in pDpsim, often exceeding the OB input correlation (gray shaded area). (C) Firing rates in response to morphed odors averaged across assembly neurons (learned odor, full line) or pseudo-assembly neurons (novel odor, dashed line) as a function of similarity between the presented odor and learned odor L (see A). (D) Excitatory input from the OB averaged over assembly neurons or non-assembly neurons. (E) Sum of inhibitory and excitatory currents evoked by other pDpsim neurons (recurrent input), averaged over assembly or non-assembly neurons. (F) Absolute inhibitory and excitatory recurrent currents averaged over assembly neurons. (B–F) Averages over eight networks.

Pattern completion: additional results.
(A) Artificial reactivation of E assemblies. During 6 Hz baseline activity of the olfactory bulb (OB), a subset of the assembly neurons was artificially reactivated by current injection (500 ms, 28 pA). Mean firing rates were quantified in the injected assembly neurons (i), in the remaining, non-injected assembly or pseudo-assembly neurons (ii), and in the non-assembly neurons (iii) as a function of time. The orange bar indicates duration of current injection. Average over 10 assemblies. n = 8 networks (mean ± SD). (B) Correlation between activity patterns across E neurons (output patterns) evoked by a series of input patterns representing a morph of one learned odor into another learned odor. Correlations between output patterns are plotted as a function of the correlation between the corresponding OB patterns. (C) Absolute value of the inhibitory and excitatory recurrent currents averaged over non-assembly neurons (see Figure 3F for the average over assembly neurons).
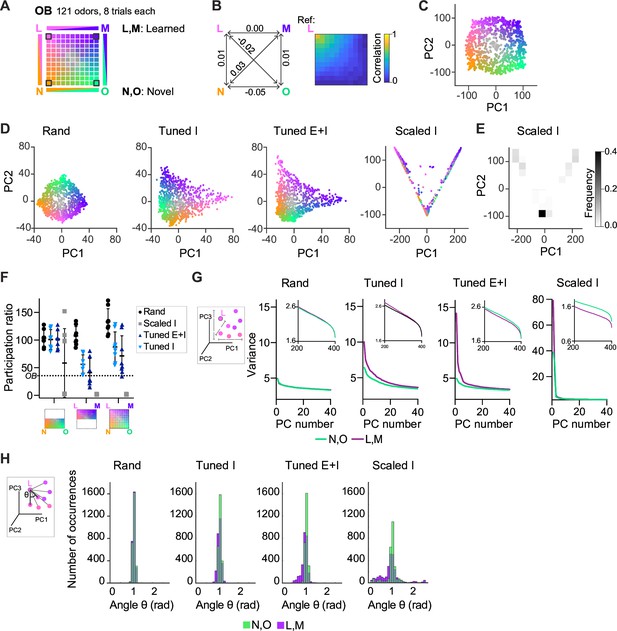
Geometry of odor representations in pDpsim.
(A) Odor subspace delineated by two learned (L, M) and two novel (N, O) pure odors at the vertices of a virtual square. Pixels within the square represent odor mixtures. (B) Left: Pearson correlations between olfactory bulb (OB) activity patterns defining pure odors. Right: Correlation between one pure odor (L; top left vertex) and all other odors. The odor from one vertex gradually morphs into the odor from another vertex. (C) Projection of activity patterns in the OB onto the first two principal components (PCs). Colors represent patterns in the odor subspace as shown in (A, D). Projection of activity patterns in pDpsim in response to the odor subspace onto the first two PCs. Representative examples of different pDp networks. (E) Density plot showing distribution of data points and demonstrating clustering at distinct locations in PC space for Scaled I networks. (F) Quantification of dimensionality of neural activity by the participation ratio: activity evoked by novel odors and related mixtures (left), activity evoked by learned odors and related mixtures (center), and activity evoked by all stimuli (right). Each data point represents one network (n = 8, mean ± SD); dotted line represents the participation ratio of OB activity. (G) Variance along the first 40 PCs extracted from activity patterns in different networks. Insets: Variance along PCs 200–400. (H) Angles between edges connecting a pure odor response and related versions thereof (inset). The analysis was performed using the first 400 PCs, which explained >75% of the variance in all networks. n = 168 angles per pure odor in each of 8 networks (Methods). Similar results were obtained in the full-dimensional space.
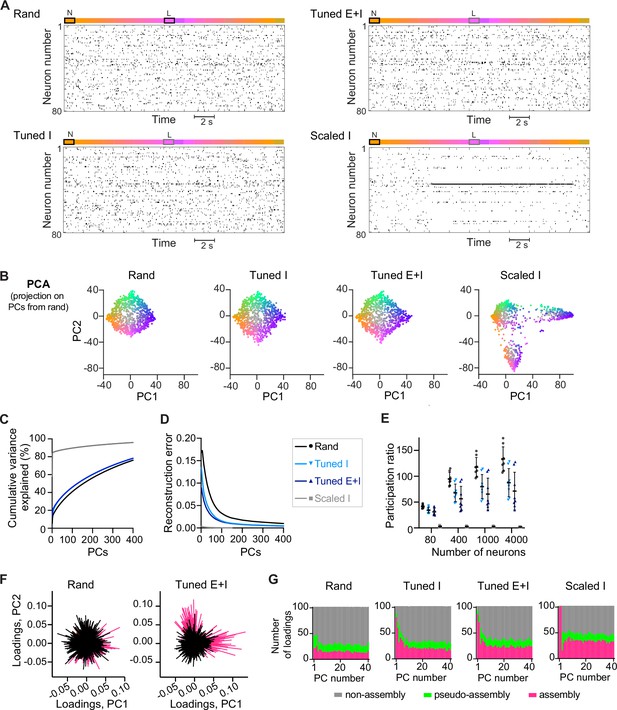
Transformations and dimensionality of activity patterns: additional results.
(A) Spike raster of 80 E neurons in response to a trajectory within the odor subspace (Figure 4A) including one pure learned and one pure novel odor. (B) Projection of activity patterns representing the odor subspace (Figure 4A) onto the first two principal components (PCs) of the corresponding rand networks (representative examples of one network each). (C) Scree plot for the principal component analysis (PCA) results shown in Figure 4D. (D) Error in the reconstruction of odor-evoked activity patterns as a function of the number of PCs. Euclidean distances between all pairs of activity patterns were calculated in the full-dimensional state space (Df) and in reduced-dimensional embedding spaces (Dl). The reconstruction error was defined as 1 – (correlation between Df and Dl). (E) Participation ratio of the neural activity sampled from different numbers of neurons (50 iterations). (F) Loading plot: Contribution of neurons to the first two PCs of a rand and a Tuned E+I network (Figure 4D). Each line represents one neuron and neurons that are part of the assemblies representing the two learned odors are color-coded in magenta. (G) For each network and PC, the 100 E neurons with the highest absolute loadings were selected and grouped into three categories: neurons part of the two assemblies representing the learned odors, neurons part of the two ‘pseudo-assemblies’ representing the two novel odors, and the remaining neurons (non-assembly).
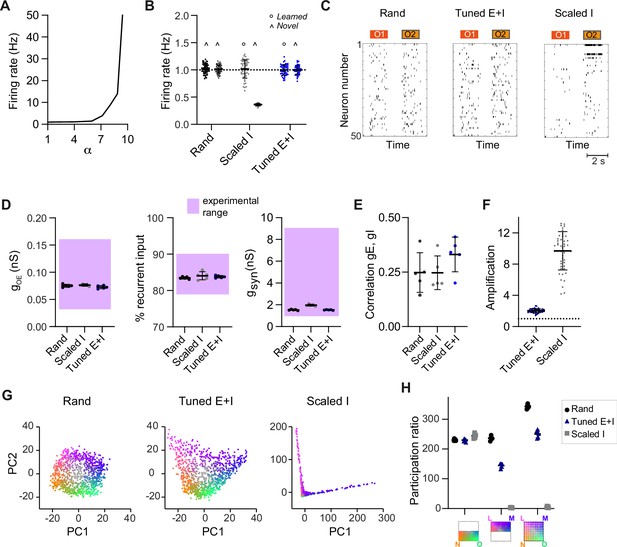
Geometry and dynamics in a simple model with equal parameters for excitation and inhibition.
(A) Firing rates averaged over all E neurons as a function of α (mean across five networks). (B) Mean firing rate in response to learned odors or novel odors. Each data point represents one network-odor pair (n = 5 networks, 10 odors). Mean ± SD. (C) Spike raster plots showing responses of 50 E neurons to 2 odors (O1: novel odor; O2: learned odor). (D) Left: Synaptic conductance contributed by afferents from the olfactory bulb (OB) during odor stimulation (gOE). Middle: Total odor-evoked synaptic conductance gsyn. Right: Percentage of E input contributed by recurrent connections during odor stimulation. Each dot represents one network (average over 10 odors); n = 5 networks. (E) Co-tuning: correlation between time-averaged E and I conductances in response to different odors, average across neurons. (F) Amplification within assemblies, calculated as the ratio between mean firing rates in response to learned odors averaged across assembly neurons in a structured network (Scaled I or Tuned E+I) and the same neurons in the corresponding rand network. (G) Projection of activity patterns in pDpsim in response to the odor subspace described in Figure 4 onto the first two principal components (PCs). Representative examples of different networks. (H) Participation ratio (similar to Figure 4F): activity evoked by novel odors and related mixtures (left), activity evoked by learned odors and related mixtures (center), and activity evoked by all stimuli (right).
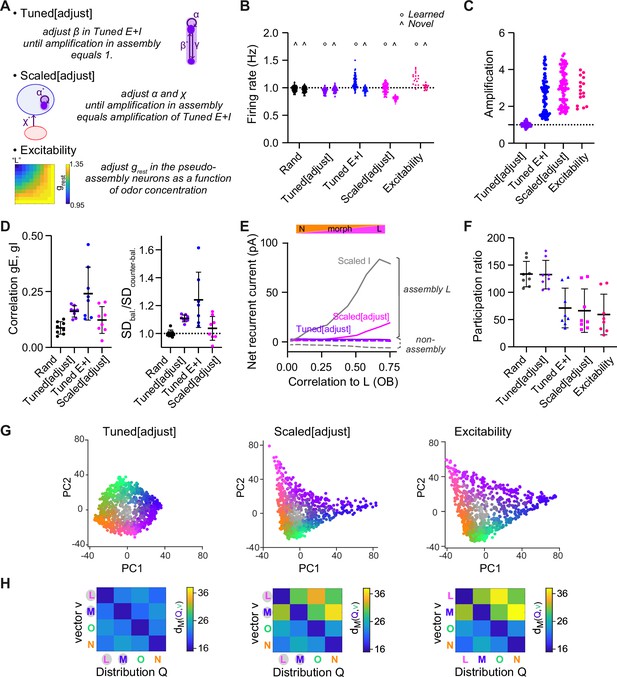
Manipulating amplification within assemblies.
(A) Overview of modified pDpsim networks that were generated to manipulate amplification of activity within assemblies. (1) Tuned[adjust]: in existing Tuned E+I networks, the probability of I-to-E connections (β) is further increased until the mean activity within assemblies is similar to the activity of the corresponding pseudo-assemblies in rand networks. (2) Scaled[adjust]: Parameters α and χ are set such that the mean activity within assemblies matches the mean activity in assemblies of Tuned E+I networks. (3) Excitability: in rand networks, during presentation of odor L or M, the resting conductance grest of the corresponding pseudo-assembly neurons is decreased until their mean activity matches the mean activity of the Tuned E+I assembly. During mixture presentation, grest decreases linearly with the concentration of the odor. (B) Mean firing rate in response to learned or novel odors (see Figure 2F). Each data point represents one network-odor pair (n = 8 networks, 10 odors). In Scaled[adjust], mean firing rates for novel odors were lower than for learned odors. (C) Amplification within assemblies, calculated as the ratio between mean firing rates in response to learned odors averaged across assembly neurons (structured network) and the corresponding pseudo-assembly neurons (rand network); see Figure 2G. (D) Quantification of E/I co-tuning. Left: Correlation between time-averaged E and I conductances in response to different odors, average across neurons. Right: Ratio of dispersion of joint conductances along balanced and counter-balanced axes (see Figure 2H, I). Note that E/I co-tuning remained weak in Scaled[adjust] networks, inconsistent with experimental observations. (E) Sum of recurrent inhibitory and excitatory currents averaged over assembly or non-assembly neurons (see Figure 3E). In Tuned E+I and Scaled[adjust] networks, recurrent E inputs in assemblies slightly exceeded I inputs in the vicinity of learned odors. In Tuned[adjust], recurrent E and I inputs canceled out. (F) Quantification of dimensionality of neural activity by the participation ratio (see Figure 4F): activity evoked by the odor subspace. Each data point represents one network (n = 8). Mean ± SD. (G) Projection of activity patterns in response to the odor subspace onto the first two principal components (PCs) (representative examples of different networks; see Figure 4D). (H) The Mahalanobis distance dM between one activity vector (v) and reference classes (Q) (Methods and Figure 5B). dM was computed based on activity across subsets of 80 E neurons drawn from the four (pseudo-) assemblies with equal probability.
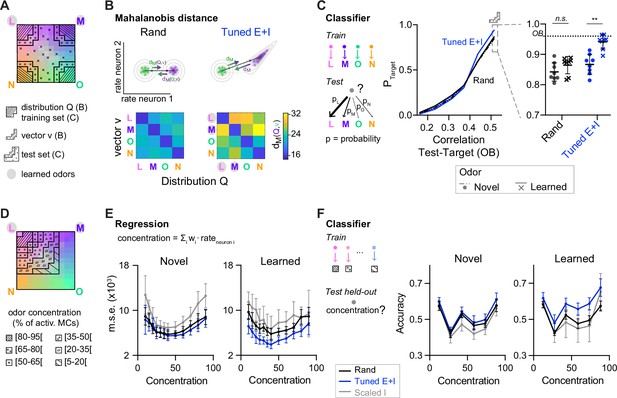
Distance relationships and classification of odor representations.
(A) Odor-evoked activity patterns used as class distributions and vectors (B) or training and test sets (C). Same odor subspace as in Figure 4. (B) Top: Schematic illustration of Mahalanobis distance dM. Bottom: dM between one activity vector (v) and reference classes (Q) in rand and Tuned E+I networks. dM was computed based on the activity patterns of 80 E neurons drawn from the four (pseudo-) assemblies. Average of 50 draws. Note that dM between patterns related to a learned odor and non-matching reference classes was higher in Tuned E+I networks. (C) Pattern classification probability quantified by quadratic discriminant analysis (QDA). PTarget quantifies the probability that an activity pattern from the test set (odor mixtures, see A) is assigned to a target class from the training set (pure or closely related odor; see A). Left: Classification probability as a function of the similarity (Pearson correlation) between the test and target odors in the olfactory bulb (OB) (input patterns). Note enhanced classification probability for patterns evoked by odors similar to learned odors in Tuned E+I networks. Right: Classification probability for patterns similar to the training set (see A). Each data point represents one network (n = 8, mean ± SD; Wilcoxon signed-rank test, **: p < 0.01). (D) The odor subspace of Figure 4 was subdivided in classes reflecting different concentrations of one of the pure odors (Methods). Odor concentration is defined here as the percentage of the 150 mitral cells representing a given odor that are activated. (E) The concentration of a given odor was regressed against the mean firing rates of a subset of neurons (Methods). Mean square error (squared difference between the actual concentration and the estimated concentration). (F) Accuracy of a linear support vector machine (SVM) in predicting the concentration of a novel (left) or learned odor (right) in a mixture. Each data point represents one network (n = 8, mean ± SD).
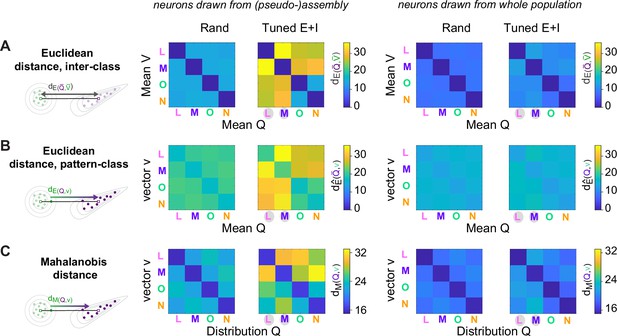
Further analyses of pattern distances: uncorrelated odors.
Differences in dM between rand and Tuned networks may involve differences in the distance between class centers and/or differences in intra-class variability. To dissect the contributions of these effects we compared three distance measures:
(1) The Euclidean distance between class centers:
.
(2) The mean Euclidean distance between patterns of one class and the center of another class ():
.
(3) The Mahalanobis distance dM:
.
Here, and are the centers (average patterns) of classes V and Q, respectively; v is a vector from V = [v1, v2, …, vn], and is the inverse of the covariance matrix of the neuronal population within reference class Q. Note that corresponds to dM without normalization by variability (covariance). (A) Analysis of dE. Left: dE in rand and Tuned E+I networks based on 80 E neurons drawn from (pseudo-) assemblies. Right: Same based on 80 E neurons drawn from the entire population. Note that dE between learned and other odors was increased in Tuned E+I networks as compared to rand networks, particularly when neurons were drawn from assemblies. (B) Equivalent plots for Note that distances were increased nearly symmetrically, similar to dE. (C) Equivalent plots for dM (same plots as in Figure 5B). Note that dM was increased asymmetrically. These observations show that the changes in dM relative to rand networks involved an increase in the distance between class centers (dE) and a non-isotropic change in intra-class variability (comparison between and dM). These effects were prominent when E neurons were drawn from assemblies. An important contribution to the increase in dM in the direction from learned odors to reference classes representing novel odors was made by the increased distance between class centers. In the other direction, dM was smaller, implying that variability in the reference class was higher. Nonetheless, variability in the relevant direction did not fully counteract the increased distance between class centers in Tuned E+I networks. As a consequence, dM was still increased slightly relative to the corresponding rand networks. Most of these effects were still observed, albeit weakly, when E neurons were drawn from the whole population.
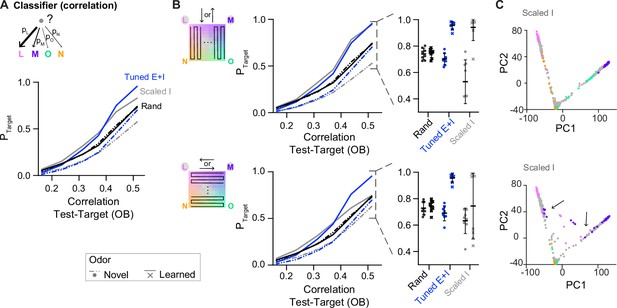
Classification of odor representations (template matching).
(A) Pattern classification probability quantified by template matching (see Methods). PTarget quantifies the probability that an activity pattern from the test set is assigned to a target class from the training set (see Figure 5A) and is plotted as a function of the similarity (Pearson correlation) between the test and target odor patterns in the olfactory bulb (OB). Unlike quadratic discriminant analysis (QDA), template matching can also be applied to outputs of Scaled networks. Note enhanced classification probability for patterns evoked by odors similar to learned odors in Tuned E+I networks, and to a lesser extent in Scaled networks. (B) The dataset was divided into two categories, depending on the trajectory in the odor subspace (insets; n = 484 activity patterns each), and template matching was performed again on each of the generated datasets. Note that learned odors were presented further apart in time in the top panels than in the bottom panels. Left: PTarget as a function of similarity in the OB, see panel A. Right: Classification probability for patterns similar to the training set (see A). Note that odor classification by Scaled networks depends on the trajectories in the odor subspace. (C) Projection of activity patterns in response to the odor subspace onto the first two principal components (PCs) in Scaled networks. Odor representations depend on stimulus history: note the reduced separation between representations of different odor classes during trajectories morphing one learned odor into another learned odor (arrows). This effect arises from the attractor dynamics of the networks.
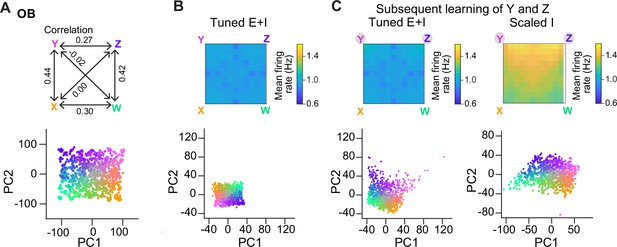
Representation of correlated patterns and resilience against additional memories.
(A) Subspace delineated by four positively correlated odors (see Methods). Top: Correlations between pure odors. Bottom: Projection of olfactory bulb (OB) activity patterns onto the first two principal components (PCs). (B) Firing rates (top) and PC projection of output activity of a Tuned E+I network with 15 E/I assemblies that did not represent any of the four pure odors of the subspace. (C) Firing rates (top) and PC projection of output activity (bottom) after creation of two additional assemblies representing two of the pure odors (Y and Z). Left: Tuned E+I network. Right: Scaled I network. Note that in the Scaled I network, but not in the Tuned E+I network, firing rates evoked by newly learned odors were increased and patterns evoked by these odors were not well separated in PC space.

Further analyses of pattern distances: correlated odors.
(A–C) Pattern distances in Tuned E+I networks with (right) and without (left) two additional assemblies representing Y and Z (see Figure 6) based on 80 E neurons drawn from assemblies. Similar analysis as in Figure 5—figure supplement 1, but for the odor subspace described in Figure 6. (A) dE. (B) . (C) dM. (D) Pattern classification probability quantified by quadratic discriminant analysis (QDA). PTarget quantifies the probability that an activity pattern from the test set is assigned to a target class from the training set (pure or closely related odor; see also Figure 5A, C).

Schematic of geometric transformations.
(A) Randomly connected networks tend to preserve the geometry of coding space. Such networks can support neuronal computations, for example, by projecting activity patterns in a higher-dimensional coding space for pattern classification. (B) We found that balanced networks with E/I assemblies transform the geometry of representations by locally restricting activity onto manifolds. These networks stored information about learned inputs while preserving continuity of the coding space. Such a geometry may support fast classification, continual learning and cognitive computations. Note that the true manifold geometry cannot be visualized appropriately in 2D because activity was ‘focused’ in different subsets of dimensions at different locations of coding space. As a consequence, the dimensionality of activity remained substantial. (C) Neuronal assemblies without precise balance established discrete attractor states, as observed in memory networks that store information as discrete items. Networks establishing locally defined activity manifolds (B) may thus be considered as intermediates between networks generating continuous representations without memories (A) and classical memory networks with discrete attractor dynamics (C).
Tables
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Software, algorithm | Matlab | Mathworks | https://ch.mathworks.com (RRID:SCR_001622) |
Values of the neuronal parameters.
The superscripts indicate the reference where the experimental measurements can be found.
| Neuronal parameters | Symbol | Value | ||
|---|---|---|---|---|
| Excitatory neuron | Inhibitory neuron | Simple model | ||
| Membrane time constant | 85 ms*,† | 50 ms† | 68 ms | |
| Resting conductance | 1.35 nS* | 0.9 nS | 1.1 nS | |
| Resting potential | –60 mV*,† | –65 mV | –62 mV | |
| Excitatory reversal potential | 0 mV* | 0 mV | 0 mV | |
| Inhibitory reversal potential | –70 mV* | –70 mV | –70 mV | |
| Spiking threshold | –38 mV* | –45 mV | –41 mV | |
| Reset potential | –60 mV | –65 mV | –62 mV | |
| Refractory period | 8 ms | 8 ms | 8 ms | |
| Adaptation time constant | 40 ms | / | 20 ms | |
| Subthreshold adaptation | 1 nS | / | 0.5 nS | |
| Spike-triggered adaptation | 10 pA | / | 5 pA | |
-
*
-
†
Values of the connectivity parameters of different networks {probability pYX and synaptic strength YX in pS}.
| Network structure | OB → E | OB → I | E → E | E → I | I → E | I → I |
|---|---|---|---|---|---|---|
| A (n = 5) | {0.02, 128} | {0.01, 68} | {0.05, 128} | {0.04, 68} | {0.05, 480} | {0.04, 250} |
| B (n = 5) | {0.02, 128} | {0.01, 66} | {0.05, 128} | {0.04, 66} | {0.05, 450} | {0.04, 210} |
| C (n = 5) | {0.02, 128} | {0.01, 68} | {0.05, 108} | {0.02, 80} | {0.05, 520} | {0.02, 310} |
| D (n = 5) | {0.03, 95} | {0.02, 42} | {0.05, 128} | {0.04, 58} | {0.05, 590} | {0.04, 270} |
| Simple (n = 5) | {0.03, 160} | {0.03, 160} | {0.025, 370} | {0.025, 370} | {0.1, 1010} | {0.1, 1010} |
Percentage of mitral cells out of the 150 mitral cells defining one pure odor (top left corner) that are activated in mixtures.
Percentages may be interpreted as relative odor concentration. Values given here are for uncorrelated pure odors.
| 100 | 90 | 80 | 70 | 60 | 50 | 40 | 30 | 20 | 10 | 0 |
| 90 | 90 | 80 | 70 | 60 | 50 | 40 | 30 | 15 | 5 | 0 |
| 80 | 80 | 70 | 60 | 50 | 40 | 35 | 25 | 15 | 5 | 0 |
| 70 | 70 | 60 | 50 | 50 | 35 | 30 | 20 | 15 | 5 | 0 |
| 60 | 60 | 50 | 50 | 40 | 30 | 25 | 20 | 15 | 5 | 0 |
| 50 | 50 | 40 | 35 | 30 | 25 | 25 | 15 | 10 | 5 | 0 |
| 40 | 40 | 35 | 30 | 25 | 25 | 15 | 10 | 10 | 5 | 0 |
| 30 | 30 | 25 | 20 | 20 | 15 | 10 | 10 | 5 | 5 | 0 |
| 20 | 15 | 15 | 15 | 15 | 10 | 10 | 5 | 5 | 5 | 0 |
| 10 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Percentage of activated cells available for selection for uncorrelated pure odors.
C is obtained by multiplying the values by 1.5.
| 100 | 100 | 100 | 90 | 80 | 70 | 60 | 50 | 40 | 30 | 0 |
| 100 | 100 | 100 | 90 | 80 | 70 | 60 | 50 | 35 | 25 | 0 |
| 100 | 100 | 90 | 60 | 70 | 60 | 55 | 45 | 35 | 25 | 0 |
| 90 | 90 | 80 | 70 | 70 | 55 | 50 | 40 | 35 | 25 | 0 |
| 80 | 80 | 70 | 70 | 60 | 50 | 45 | 40 | 35 | 25 | 0 |
| 70 | 70 | 60 | 55 | 50 | 45 | 45 | 35 | 30 | 25 | 0 |
| 60 | 60 | 55 | 50 | 45 | 45 | 35 | 30 | 30 | 25 | 0 |
| 50 | 50 | 45 | 40 | 40 | 35 | 30 | 30 | 25 | 25 | 0 |
| 40 | 35 | 35 | 35 | 35 | 30 | 30 | 25 | 25 | 25 | 0 |
| 30 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Parameters of structured networks.
| Figures 2—6 | Figure 4—figure supplement 3 (mean) | |
|---|---|---|
| Scaled I | α = 5, χ = 1.4 | Scaled[adjust]: α = 3.7, χ = 1.07 |
| Tuned I | α = 5, β = 18 | / |
| Tuned E+I | α = 5, β = 4, γ = 3 | Tuned[adjust]: α = 5, β = 11.5, γ = 3 |





