Figures and data in Current CRISPR gene drive systems are likely to be highly invasive in wild populations

Figures
Tables
Additional files

11 figures, 3 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

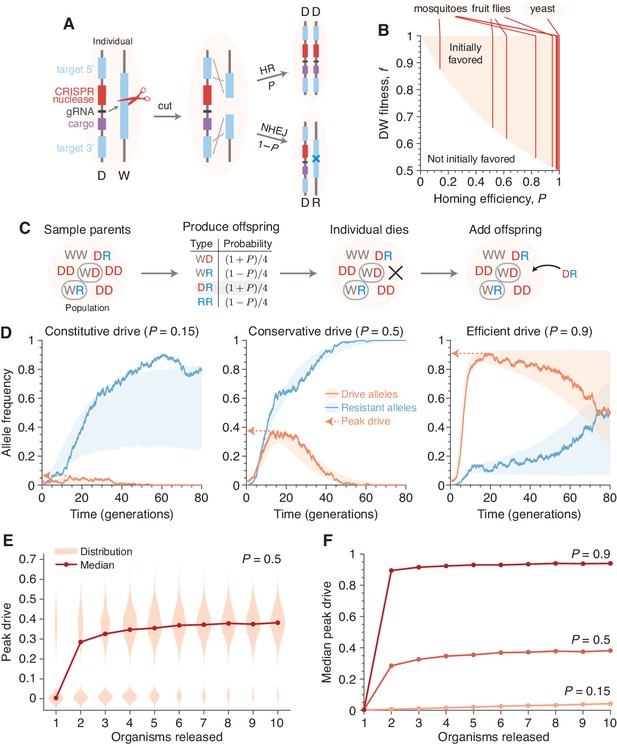
Existing alteration-type CRISPR gene drive systems should invade well-mixed wild populations.

(A) Typical construction and function of alteration-type CRISPR gene drive systems. A drive construct (D), including a CRISPR nuclease, guide RNA (gRNA), and ‘cargo’ sequence, induces cutting at a wild-type allele (W) with homology to sequences flanking the drive construct. Repair by homologous recombination (HR) results in conversion of the wild-type to a drive allele, or repair by nonhomologous end-joining (NHEJ) produces a drive-resistant allele (R). (B) Drives are predicted to invade by deterministic models when the fitness of DW heterozygotes, $f$ , and the homing efficiency, $P$ , are in the shaded region. Vertical lines indicate empirical efficiencies from Appendix 1—table 1. (C) Diagram of a single step of the gene-drive Moran process. (D) Finite-population simulations of 15 drive individuals released into a wild population of size 500, assuming conservative ( $P = 0.5$ ) or high ( $P = 0.9$ ) homing efficiencies, as well as a low-efficiency, constitutively active system ( $P = 0.15$ ). Individual sample simulations (solid lines), and 50% confidence intervals (shaded), calculated from $10^{3}$ simulations. Drive-allele frequencies red and resistant-allele frequencies blue. Peak drive, or maximum frequency reached, is illustrated by dashed lines and arrows. (E) Peak drive distributions and medians with varying numbers of individual organisms released ( $P = 0.5$ ). (F) Medians of peak drive distributions for varying homing efficiencies ( $P = 0.15$ , bottom; $P = 0.5$ , middle; $P = 0.9$ , top). Throughout, we assume neutral resistance ( $f_{W R} = f_{R R} = 1$ ) and a 10% dominant drive fitness cost ( $f_{W D} = f_{D D} = f_{D R} = 0.9$ ).

https://doi.org/10.7554/eLife.33423.003

Figure 2

Download asset Open asset

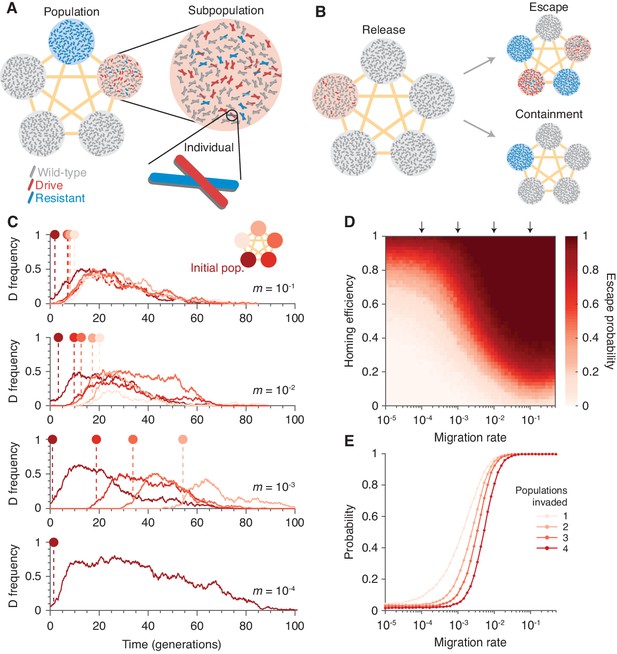
Existing CRISPR gene drive systems should invade linked subpopulations connected by gene flow.

(A) Diagram of well-mixed subpopulations (circles) linked by gene flow (edges). Individuals represented by chromosomes with wild-type (gray), drive (red), or resistant (blue) haplotypes. (B) Few drive homozygotes are released in one subpopulation. The drive escapes if it invades another subpopulation before going extinct. Otherwise it is contained. (C) Typical simulations for varying migration rates ( $m = 10^{- 1}$ , top, to $m = 10^{- 4}$ , bottom), following introduction into a single subpopulation. Lines represent drive frequencies in each subpopulation. Circles correspond to the time the drive invades a subpopulation. Population color is by invasion order, not predetermined. (D) Escape probability as a function of homing efficiency, $P$ , and migration rate, $m$ . Arrows indicate migration rates from B. Each pixel is calculated from $10^{3}$ simulations. (E) Probability of invading 1, 2, 3, or 4 additional populations (aside from the originating population, which is typically invaded), assuming a homing efficiency of $P = 0.5$ . Each data point is calculated from $10^{4}$ simulations. Throughout, we consider five subpopulations connected in a complete graph, each consisting of 100 individuals. Initially, 15 drive homozygotes are introduced into one subpopulation. Resistance is neutral ( $f_{W R} = f_{R R} = 1$ ) and the drive confers a dominant $10 %$ cost ( $f_{W D} = f_{D D} = f_{D R} = 0.9$ ).

https://doi.org/10.7554/eLife.33423.004

Figure 3

Download asset Open asset

Peak drive distributions for variable release and population sizes.

Parameters are chosen to correspond to Figure 1E: $P = 0.5$ , $f = 0.9$ and neutral resistance. Population sizes are, from light to dark, $N = 500, 1000, 2500, 5000, 10000$ . Note that $N = 500$ corresponds exactly to Figure 1E. Each distribution corresponds to $10^{3}$ simulations.

https://doi.org/10.7554/eLife.33423.005

Figure 4

Download asset Open asset

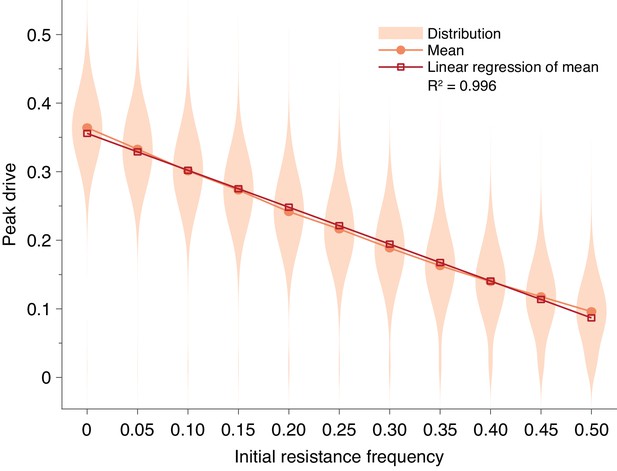
Pre-existing drive-resistant allele frequency linearly decreases peak drive.

Distributions (violin plots), means (orange, circles) and linear regression of the mean values (red, squares). Parameters are chosen to correspond to Figure 1E: $P = 0.5$ , $f = 0.9$ , neutral resistance, $N = 500$ . Each distribution corresponds to $5000$ simulations.

https://doi.org/10.7554/eLife.33423.006

Figure 5

Download asset Open asset

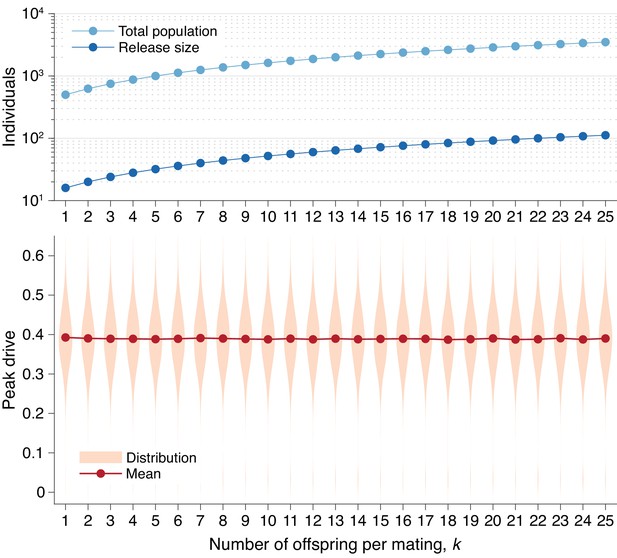
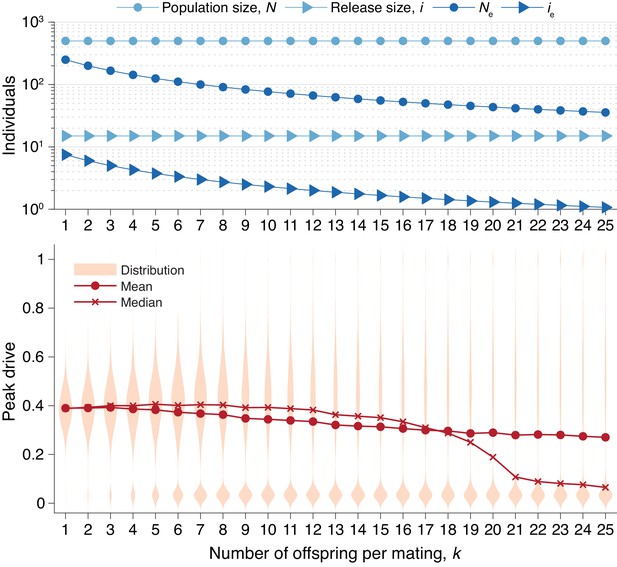
Peak drive distributions for varying numbers of offspring per mating with effective population and release sizes held constant.

(top) Population and release sizes used in the simulations below. For the case $k = 1$ , we use our usual population size of $N = 500$ with an initial release of $i = 16$ drive homozygotes. According to Equation (5), the effective total population and release sizes in this case are $N_{e} = 250$ and $i_{e} = 8$ . For other values of $k$ , we use values of $N$ and $i$ which maintain constant effective population and release sizes: $N = N_{e} (2 k + 6) / 4$ and $i = i_{e} (2 k + 6) / 4$ . These values are plotted: $N$ (light blue) and $i$ (dark blue). (bottom) Peak drive distributions assuming values of $N$ and $i$ as in the above plot. All employ $P = 0.5$ , $f = 0.9$ , and neutral resistance. Each distribution includes 5000 simulations.

https://doi.org/10.7554/eLife.33423.007

Figure 6

Download asset Open asset

Peak drive distributions for varying numbers of offspring per mating with census population and actual release sizes held constant.

(top) Population and release sizes used in the simulations below. Actual population size, $N$ (light blue, circles) and actual release size, $i$ (light blue, triangles). Note that $N = 500$ and $i = 15$ are constant. Effective values calculated via Equation (5): population size, $N_{e}$ (dark blue, circles) and release size, $i_{e}$ (dark blue, triangles). (bottom) Peak drive distributions for simulations using indicated values of $k$ and population and release sizes as depicted above. Compare with Figure 5 which holds the *effective* population and release sizes constant, whereas here we hold the *census* population and release sizes constant. All simulations employ $P = 0.5$ , $f = 0.9$ , and neutral resistance. Each distribution includes 5000 simulations.

https://doi.org/10.7554/eLife.33423.008

Figure 7

Download asset Open asset

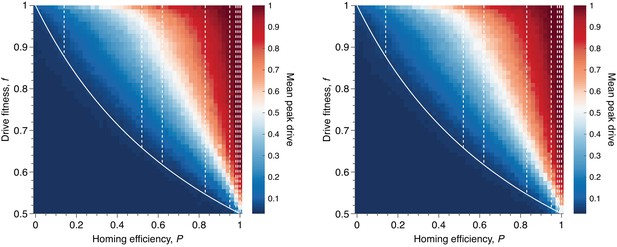
Mean peak drive for varying homing efficiency, $P$ , and drive-individual fitness values, $f$ (i.e., individuals with genotypes WD, DD, and DR), assuming that fitness affects birth rate (left) or death rate (right).

The left panel corresponds to our standard model, shown in Figure 1C, while the right panel represents a modification: parents are chosen uniformly, and individuals die with probability proportional to the inverse of their fitness. The solid white line shows the boundary from Figure 1B indicating whether the drive is predicted to invade by deterministic models. The drive is only expected to invade based on deterministic models if the fitness/homing efficiency pair lie above the boundary. The dashed white lines indicate the empirically measured homing efficiencies from Appendix 1—table 1 and Figure 1B. Each point in the grid ( $51 \times 51$ ) depicts an average of 100 simulations. Parameters used include a population size of 500, with an initial release of 15 drive homozygotes to ensure that trajectories establish. Neutral resistance is assumed throughout with no standing genetic variation.

https://doi.org/10.7554/eLife.33423.009

Figure 8

Download asset Open asset

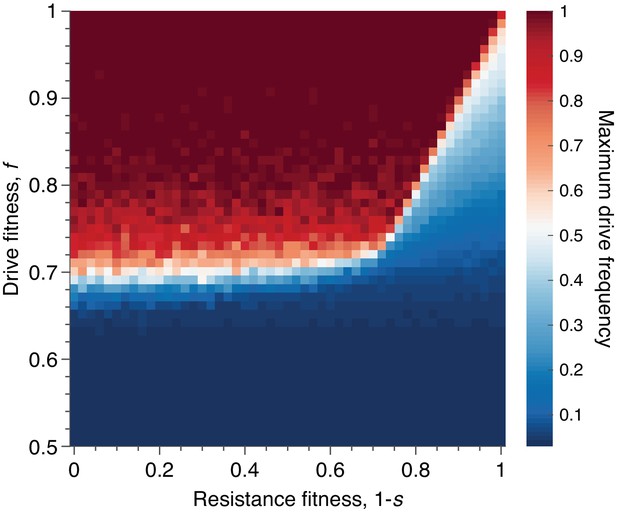
Mean peak drive for varying drive-individual fitness values, $f$ , and resistant-individual (RR) fitness values, $1 - s$ , where $s$ is the cost associated with resistance.

Each point in the grid ( $51 \times 51$ ) depicts an average of 100 simulations. Parameters used include homing efficiency $P = 0.5$ , population size of 500, with an initial release of 15 drive homozygotes to ensure that trajectories establish. Throughout we assume no standing genetic variation (i.e., the initial frequency of the resistant allele is 0).

https://doi.org/10.7554/eLife.33423.010

Figure 9

Download asset Open asset

Peak drive distributions and means for varying selfing rates in our partial selfing model.

(top) Effective drive, $P = 0.9$ . (middle) conservative drive, $P = 0.5$ , and (bottom) constitutive drive, $P = 0.15$ . Each distribution comprises $1000$ simulations. Parameters used include a population size of 500 with an initial release of 15 drive homozygotes. Neutral resistance is assumed throughout with no standing genetic variation, and the offspring number per mating is $k = 1$ .

https://doi.org/10.7554/eLife.33423.011

Figure 10

Download asset Open asset

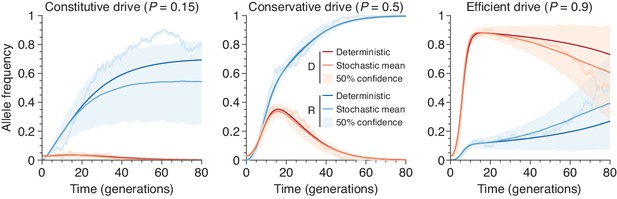
Finite-population simulations of 15 drive individuals released into a wild population of size 500, assuming low ( $P = 0.5$ ) or high ( $P = 0.9$ ) homing efficiencies, as well as a low-efficiency, constitutively active system ( $P = 0.15$ ).

Deterministic results (dark lines) and means of $10^{3}$ simulations (medium lines), individual sample simulations (light lines), and 50% confidence intervals (shaded). Drive frequencies red and resistant-allele frequencies blue.

https://doi.org/10.7554/eLife.33423.012

Figure 11

Download asset Open asset

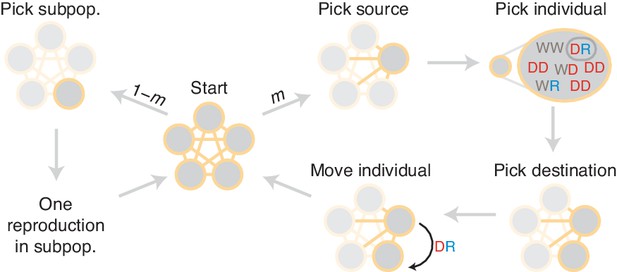
Diagram of simulation scheme.

In each time step, a migration occurs with probability $m$ , or a mating happens with probability $1 - m$ . If a migration occurs, a source population is chosen randomly proportional to its size; an individual is chosen uniformly at random, then a destination is chosen uniformly at random, and the individual is moved. If a mating occurs, the dynamics proceed as in the well-mixed case for a particular subpopulation (Figure 1C).

https://doi.org/10.7554/eLife.33423.013

Tables

Appendix 1—table 1

Empirical homing efficiencies for all CRISPR gene drive systems published to date.

Details can be found in the Appendix.

https://doi.org/10.7554/eLife.33423.016

Organism	Ref.	System name	Efficiency
Yeast	(DiCarlo et al., 2015)	ade2::sgRNA	$> 99 %$
		ade2::sgRNA + URA3	$100 %$
		sgRNA + ABD1	$100 %$
		cas9 + sgRNA	$> 99 %$
		ADE2 + sgRNA + cas9	$> 99 %$
Fruit flies	(Gantz and Bier, 2015)	$γ$ -MCR	$97 %$
	(Champer et al., 2017)	nanos	$62 %$
		vasa	$52 %$
		additional nanos	40–62%
		additional vasa	37–53%
Mosquitoes	(Gantz et al., 2015)	AsMCRkh2 (male)	$98 %$
		AsMCRkh2 (female)	$14 %$
	(Hammond et al., 2016)	AGAP011377	$83 %$
		AGAP005958	$95 %$
		AGAP007280	$99 %$

Appendix 1—table 2

Gantz et al., An. stephensi transgenic male lines.

(left) Phenotypes of G $_{3}$ progeny. (right) Phenotypes of G $_{4}$ progeny.

https://doi.org/10.7554/eLife.33423.017

G $_{3}$ crosses	$D$	$T$	Reference
$10.1$ G $_{2}$ $\times$ WT, larval	$829$	$832$	Table S3
$10.2$ G $_{2}$ $\times$ WT, larval	$3060$	$3085$	Table S4
$10.1$ G $_{2}$ $\times$ WT, adult	$833$	$836$	Table S5
$10.2$ G $_{2}$ $\times$ WT, adult	$1258$	$1274$	Table S6
Total	$5980$	$6027$	—
G $_{4}$ crosses	$D$	$T$	Reference
Cross 6, larval	$949$	$955$	Table S7
Cross 8, larval	$609$	$628$	Table S8
Cross 6, adult	$882$	$888$	Table S10
Cross 8, adult	$565$	$583$	Table S11
Total	$3005$	$3054$	—

Appendix 1—table 3

Gantz et al., An. stephensi transgenic male lines.

(left) Phenotypes of G $_{4}$ larvae. (right) Phenotypes of G $_{4}$ adults.

https://doi.org/10.7554/eLife.33423.018

G $_{4}$ larvae	$D$	$T$	Reference
Cross $1$	$28$	$48$	Table S7
Cross 2	$332$	$635$	Table S7
Cross 3	$204$	$324$	Table S8
Cross 4	$372$	$632$	Table S8
Total	$936$	$1639$	—
G $_{4}$ adults	$D$	$T$	Reference
Cross 1	$19$	$35$	Table S10
Cross 2	$306$	$554$	Table S10
Cross 3	$169$	$272$	Table S11
Cross 4	$1430$	$2500$	Table S11
Total	$1924$	$3361$	—

Additional files

Transparent reporting form: https://doi.org/10.7554/eLife.33423.014
Download elife-33423-transrepform-v1.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Charleston Noble
Ben Adlam
George M Church
Kevin M Esvelt
Martin A Nowak

(2018)

Current CRISPR gene drive systems are likely to be highly invasive in wild populations

eLife 7:e33423.

https://doi.org/10.7554/eLife.33423

Share this article

Cite this article

Existing alteration-type CRISPR gene drive systems should invade well-mixed wild populations.

Existing CRISPR gene drive systems should invade linked subpopulations connected by gene flow.

Peak drive distributions for variable release and population sizes.

Pre-existing drive-resistant allele frequency linearly decreases peak drive.

Peak drive distributions for varying numbers of offspring per mating with effective population and release sizes held constant.

Peak drive distributions for varying numbers of offspring per mating with census population and actual release sizes held constant.

Mean peak drive for varying homing efficiency, P, and drive-individual fitness values, f (i.e., individuals with genotypes WD, DD, and DR), assuming that fitness affects birth rate (left) or death rate (right).

Mean peak drive for varying drive-individual fitness values, f, and resistant-individual (RR) fitness values, 1−s, where s is the cost associated with resistance.

Peak drive distributions and means for varying selfing rates in our partial selfing model.

Finite-population simulations of 15 drive individuals released into a wild population of size 500, assuming low (P=0.5) or high (P=0.9) homing efficiencies, as well as a low-efficiency, constitutively active system (P=0.15).

Diagram of simulation scheme.

Empirical homing efficiencies for all CRISPR gene drive systems published to date.

Gantz et al., An. stephensi transgenic male lines.

Gantz et al., An. stephensi transgenic male lines.

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Mean peak drive for varying homing efficiency, $P$ , and drive-individual fitness values, $f$ (i.e., individuals with genotypes WD, DD, and DR), assuming that fitness affects birth rate (left) or death rate (right).

Mean peak drive for varying drive-individual fitness values, $f$ , and resistant-individual (RR) fitness values, $1 - s$ , where $s$ is the cost associated with resistance.

Finite-population simulations of 15 drive individuals released into a wild population of size 500, assuming low ( $P = 0.5$ ) or high ( $P = 0.9$ ) homing efficiencies, as well as a low-efficiency, constitutively active system ( $P = 0.15$ ).