An image reconstruction framework for characterizing initial visual encoding
- Department of Psychology, University of Pennsylvania, United States
Figures
Figure 1
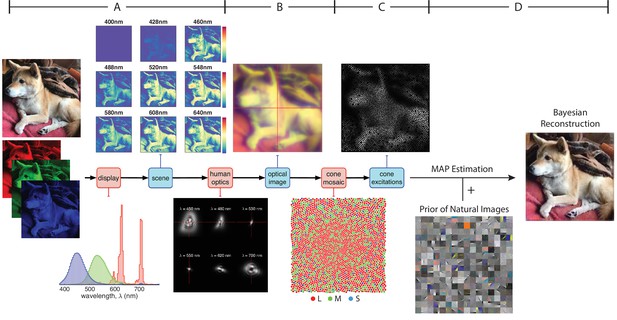
Model of the initial visual encoding and Bayesian reconstruction from cone mosaic excitation.
(A) The visual stimulus, in our case a natural image in RGB format, is displayed on a simulated monitor, which generates a hyperspectral scene representation of that image. (B) The hyperspectral image is blurred with a set of wavelength-dependent point-spread functions typical of human optics. We also account for spectral transmission through the lens and the macular pigment. This process produces the retinal image at the photoreceptor plane. (C) The retinal image is then sampled by a realistic cone mosaic, which generates cone excitations (isomerizations) for each cone. The trial-by-trial variability in the cone excitations is modeled as a Poisson process. (D) Our Bayesian reconstruction method takes the pattern of cone excitations as input and estimates the original stimulus (RGB image) based on the likelihood function and a statistical model (prior distribution) of natural images (see Materials and methods).
Figure 2
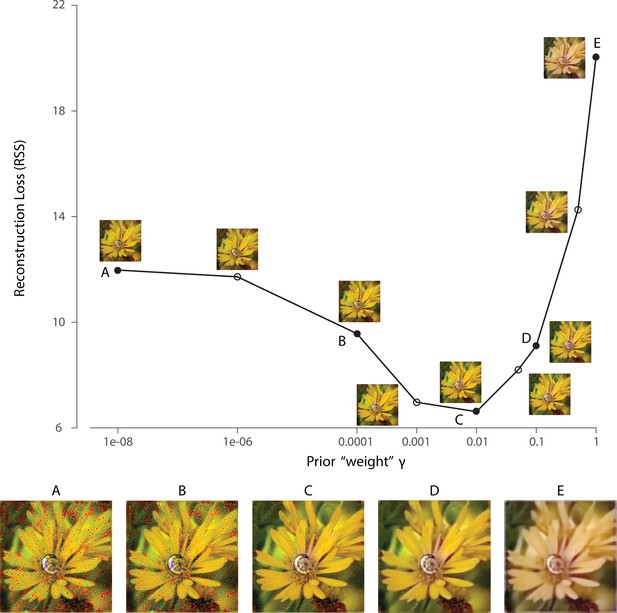
Effect of prior weight on reconstructed image.
Reconstruction error for an example natural image using a 1 deg foveal mosaic and root sum of squared distance (RSS, y-axis) in the pixel space as the error metric, as a function of weight on the log-prior term (x-axis, see Materials and methods) in the reconstruction objective function. The reconstructed image obtained with each particular value is shown alongside each corresponding point. Image (C) corresponds to the value of obtained through the cross-validation procedure (see Materials and methods). The images at the bottom are magnified versions of a subset of the images for representative values, as indicated by the solid dots in the plot.
Figure 3
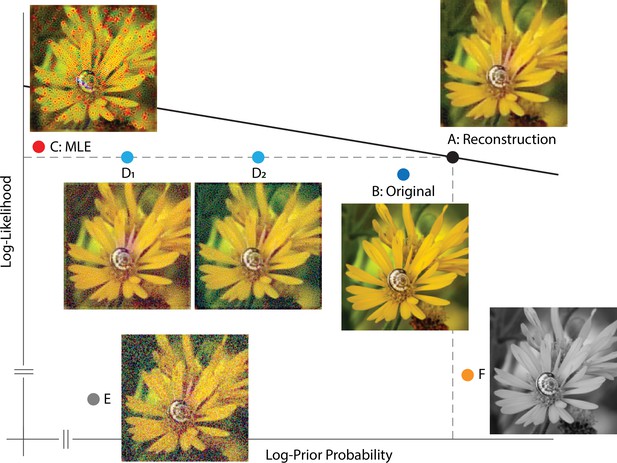
Solution space of image reconstruction.
Given a particular instance of cone excitations, we can evaluate the (log-)prior probability (x-axis) and (log-)likelihood value (y-axis) for arbitrary images. Here, a few representative images are shown together with their corresponding location in a log-prior, log-likelihood coordinate system. (A) The optimal MAP reconstruction obtained via the reconstruction algorithm. The solid line shows , with the value of evaluated at the optimal reconstruction and with the value of matched to that obtained through cross-validation. (B) Original input image (ground truth). (C) A reconstruction generated by maximum likelihood estimation (MLE, set ). Note that the maximum likelihood reconstruction shown is not unique, since adding any pattern from the null space of the likelihood matrix leads to a different reconstruction with the same maximum likelihood. Here one arbitrarily chosen MLE reconstruction is shown. (D) Optimal reconstruction, corrupted by patterns randomly sampled from the null space of the likelihood render matrix (see Materials and methods). These have the same likelihood as the optimal reconstruction, but lower prior probability. (E) Optimal reconstruction, corrupted by white noise in RGB space. (F) Grayscale version of the optimal reconstruction.
Figure 4 with 2 supplements
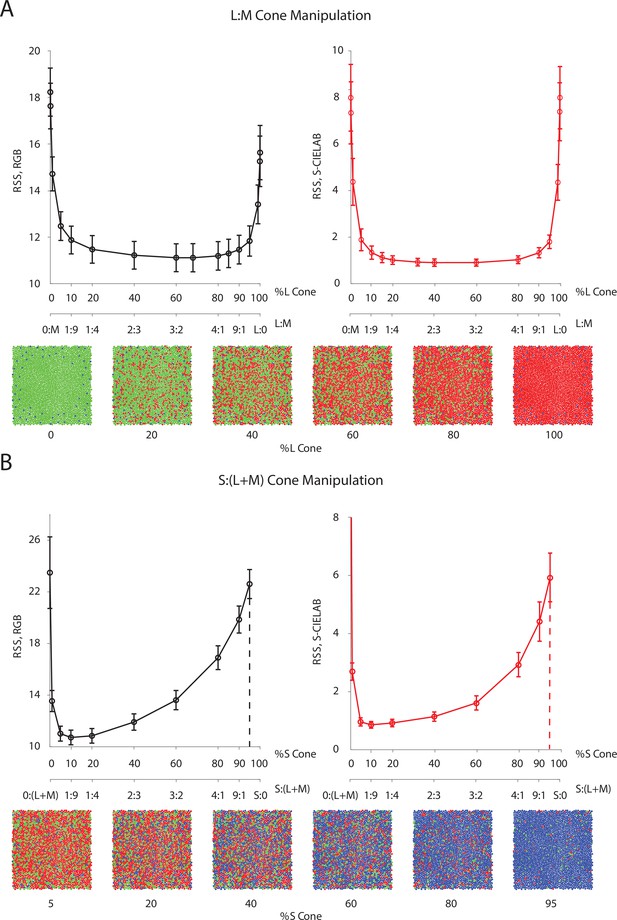
Effect of the allocation of retinal cone types on reconstruction.
Average image reconstruction error from a 1 deg foveal mosaic on a set of natural images from the evaluation set, computed as root sum of squares (RSS) distance in the RGB pixel space (y-axis, left panels) and the S-CIELAB space (y-axis, right panels), as a function of different allocations of retinal photoreceptor (cone) types in the mosaic. (A) Average (over evaluation images) reconstruction error as a function of %L cone (top x-axis), or L:M cone ratio (bottom x-axis). Example mosaics with different %L values are shown below the plot. Error bars indicate ±1 SEM. (B) Average reconstruction error as a function of %S cone (top x-axis), or S:(L + M) cone ratio (bottom x-axis). Example mosaics with different %S values are shown below the plot. Error bars indicate ±1 SEM across sampled images. See Figure 4—figure supplement 2 for a replication of the same analysis with hyperspectral images.
Figure 4—figure supplement 1
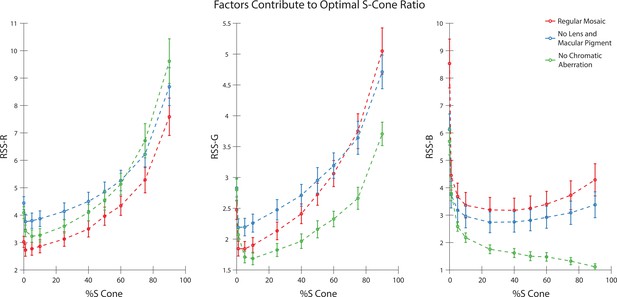
Factors that contribute to optimal S cone proportion.
Average reconstruction error as a function of S-cone proportion, computed as RSS of pixel values for the R- (left), G- (middle), and B-planes (right), respectively. Under typical conditions (red), a low S-cone ratio is optimal for all three planes. Removing lens pigment and macular pigment from the simulations (blue) increases the SNR of the S cones by increasing their average quantum catch, but has little effect on the optimal S-cone proportion for any of the image planes. Correcting chromatic aberration (green) while retaining lens pigment and macular pigment greatly improves the information provided by the S cones for the B-plane, but not for the R- and G- planes. Error bars indicate ±1 SEM.
Figure 4—figure supplement 2
Effect of the allocation of retinal cone types on reconstruction of hyperspectral images.
Average reconstruction error as a function of L-cone proportion (top) and S-cone proportion (bottom), computed as RSS of pixel values over space and wavelength, for a set of evaluation hyperspectral images of size of and 15 uniform wavelength sample between 420 nm and 700 nm (see Materials and methods). Error bars indicate ±1 SEM. The results corroborated our main conclusion obtained with RGB images, shown in Figure 4.
Figure 5 with 1 supplement
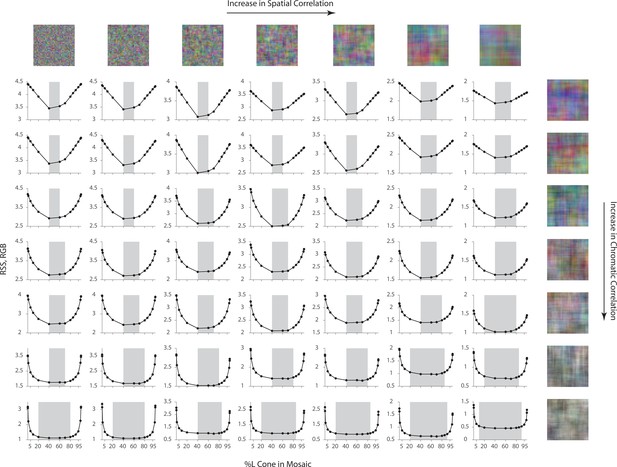
Effect of spatial and chromatic correlation on the optimal allocation of photoreceptors.
Average image reconstruction error from a half-degree square foveal mosaic on different sets of synthetic images, computed as root sum of squares (RSS) distance in the RGB pixel space, as a function of %L cone (L:M cone ratio) of the mosaic (i.e. similar to Figure 4A, left column). The shaded areas represent %L values that correspond to RSS values within a +0.1 RSS margin of the optimal (minimum RSS) point. Within each panel, synthetic images were sampled from a Gaussian distribution with specified spatial and chromatic correlation, as indicated by example images on the top row and rightmost column, and reconstruction was performed with the corresponding Gaussian prior (see Materials and methods). The overall RSS is reduced compared to Figure 4 due to the smaller image size used and the fact that the images were drawn from a different prior, as well as because the prior used in reconstruction exactly describes the images for this case. In addition, reconstruction error bars are negligible due to the large image sample size used.
Figure 5—figure supplement 1
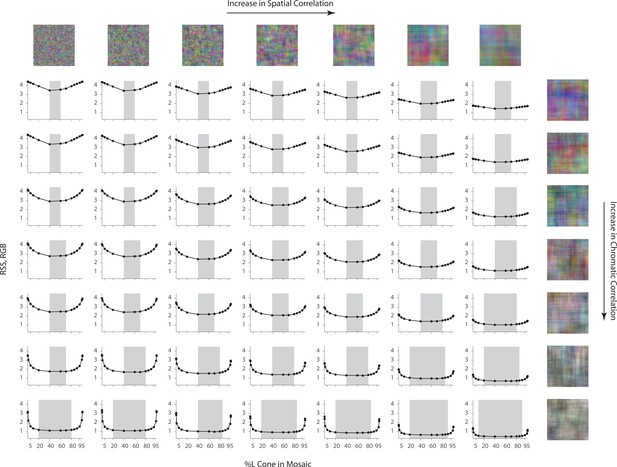
Effect of spatial and chromatic correlation on the optimal allocation of photoreceptors (with matched y-axis).
Same as Figure 5 but with matched y-axis to highlight the overall magnitude of errors across the different conditions. Average image reconstruction error from a half-degree square foveal mosaic on different sets of synthetic images, computed as root sum of squares (RSS) distance in the RGB pixel space, as a function of %L cone (L:M cone ratio) of the mosaic The shaded areas represent %L values that correspond to RSS values within a +0.1 RSS margin from the optimal (minimum RSS) point.
Figure 6
Visualization of the effect of dichromacy.
Reconstructions of a set of example images in the evaluation set from different types of 1 degree foveal dichromatic retinal mosaics (protanopia, deuteranopia, tritanopia) together with other previously proposed methods for predicting color appearance for dichromats. (A) Our method; (B) Brettel et al., 1997; (C) Jiang et al., 2016. Cone noise was not simulated for the images shown in this figure, since the comparison methods operate directly on the input images. See Materials and methods for a brief description of the implementation of the two other methods.
Figure 7 with 1 supplement
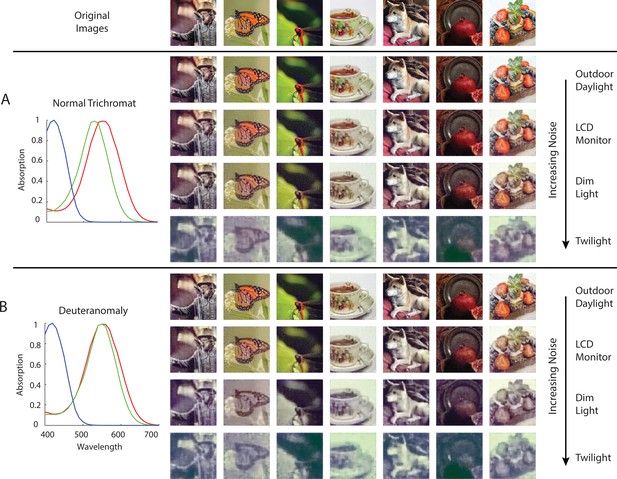
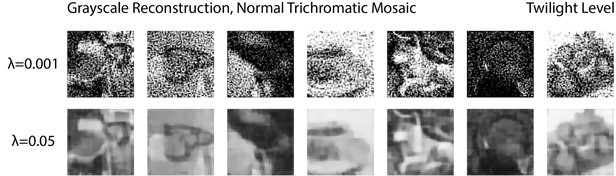
Comparison of normal and deuteranomalous observers at varying light intensities.
Image reconstructions for a set of example images in the evaluation set from 1 degree, foveal (A) normal trichromatic and (B) deuteranomalous trichromatic mosaics at four different overall light intensity levels that lead to different Poisson signal-to-noise ratios in the cone excitations. The average excitations (photo-isomerizations) per cone per 50ms integration time is chosen to be approximately 104 for Outdoor Daylight, 103 for LCD Monitor, 102 for Dim Light, and 101 for Twilight (Lewis and Zhaoping, 2006; Stockman and Sharpe, 2006). The prior weight parameter in these set of simulations was set based on a cross-validation procedure that minimizes RMSE . To highlight interaction between noise and the prior, we have also included a set of reconstructions with the prior weight set to a much lower level , see Figure 7—figure supplement 1.
Figure 7—figure supplement 1
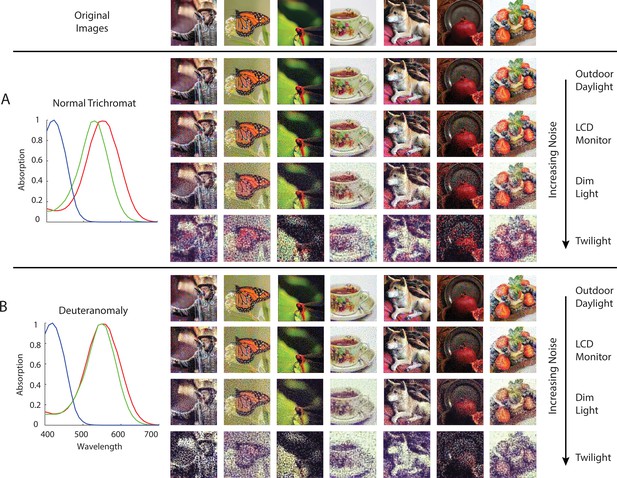
Reconstruction with a weak prior across SNR levels.
Image reconstructions for a set of example images in the evaluation set from 1 degree, foveal (A) normal trichromatic and (B) deuteranomalous trichromatic mosaics at five different overall light intensity levels that lead to different Poisson signal-to-noise ratios in the cone excitations. The average excitations (photo-isomerizations) per cone per 50ms integration time is chosen to be approximately 104 for Outdoor Daylight, 103 for LCD Monitor, 102 for Dim Light, and 101 for Twilight (Lewis and Zhaoping, 2006; Stockman and Sharpe, 2006). To highlight the effect of noise and prior, the prior weight was set to a much lower level than the optimal value used for the results shown in Figure 7.
Figure 8 with 4 supplements
Image reconstruction with optics/mosaic at different retinal eccentricities.
Image reconstructions for a set of example images in the evaluation set from 1 degree patches of mosaic at different retinal eccentricities. The coordinates at the top of each column indicate the horizontal and vertical eccentricity of the patch used for that column. The image at the top left of each column shows a contour plot of the point-spread function relative to an expanded view of the cone mosaic used for that column, while the image at the top right of each column shows the full 1 degree mosaic (see Figure 8—figure supplement 1 for an enlarged view of the mosaic and optics).
Figure 8—figure supplement 1
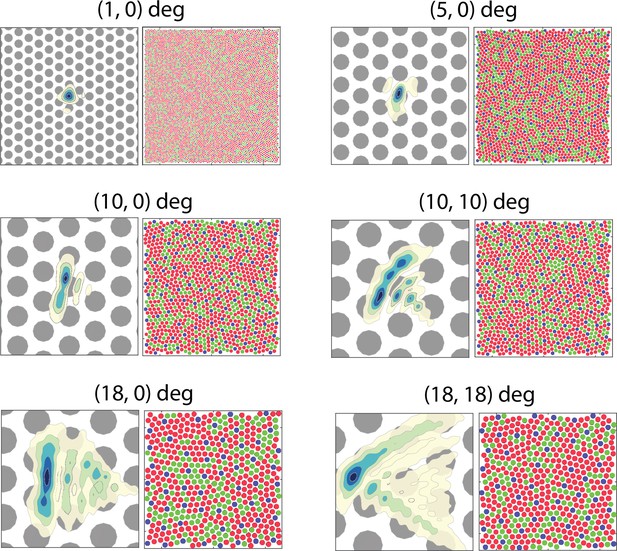
Optics and cone mosaic at different retinal eccentricities.
Enlarged view of the top panels of Figure 8. The coordinates at the top of each pair indicate the horizontal and vertical eccentricity of the retinal patch. The left image of each pair shows a contour plot of the point-spread function relative to an expanded view of the cone mosaic, while the right image of each pair shows the full 1 degree mosaic used in the simulation.
Figure 8—figure supplement 2
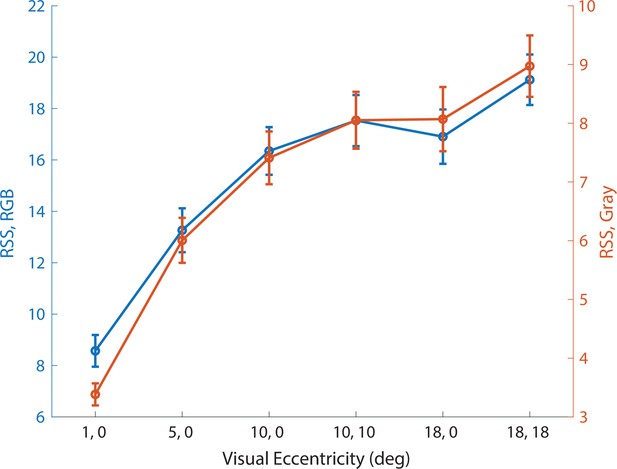
Reconstruction error at different visual eccentricities.
Average image reconstruction error, computed as RSS of pixel values for both the RGB images (left y-axis), and corresponding gray scale images to measure the spatial error, define as the first PC based on a PCA analysis of our image dataset (i.e. right y-axis), as a function of the visual eccentricity location of a 1 deg retinal mosaic. Error bars indicate ±1 SEM.
Figure 8—figure supplement 3
Image reconstruction with different point spread functions.
(A) Image reconstructions for a set of example images in the evaluation set from 1 degree patches of mosaic at (10, 10) degree eccentricity, but with PSFs sampled from different visual eccentricities as indicated by the top panel. (B) The average differential reconstruction error (i.e. difference in RSS compared to the lowest value obtained among the simulations) as a function of the eccentricity of the PSFs used. Error bars represent ±1 SEM. To separate the spatial and chromatic error, we perform a PCA analysis on the RGB images. The RSS along the first PC () corresponds to the spatial error (left axis), while the RSS along the second and third PCs () quantify the chromatic error (right axis). With the range of PSFs in our simulation, the minimal spatial error is obtained with the PSF at (10, 10) deg (i.e. the PSF that matched to the mosaic), and the minimal chromatic error is obtained with the largest PSF, corresponding to (18, 18) deg.
Figure 8—figure supplement 4
Image reconstruction at peripheral eccentricities with maximum likelihood estimation (MLE).
Image reconstructions obtained using maximum likelihood estimation for a few example images in the evaluation set from 1 degree patches of mosaic at different retinal eccentricities, as indicated at the top of each column. Note that simulation of cone excitation noise is turned off for these reconstructions. Note also that the MLE reconstructions are not unique (see Figure 3). The MLE reconstructions shown here were chosen arbitrarily as the ones converged upon by our particular numerical search algorithm.
Figure 9 with 2 supplements
Reconstruction of chromatic grating stimuli without optical aberrations.
Image reconstruction of chromatic grating stimuli with increasing spatial frequency from (A) a 0.2 deg foveal mosaic and (B) a 1 deg peripheral mosaic at (18, 18) degree retinal eccentricity, using diffraction-limited optics without LCA. The leftmost images show an expanded view of the cone mosaic relative to a contour plot of a typical point-spread function at that eccentricity. Images were modulations of the red channel of the simulated monitor, to mimic the 633 nm laser used in the interferometric experiments. The exact frequency of the stimuli being used for each condition is as denoted in the figure. For a more extended comparison between reconstructions with and without optical aberrations, see Figure 9—figure supplement 1 and Figure 9—figure supplement 2.
Figure 9—figure supplement 1
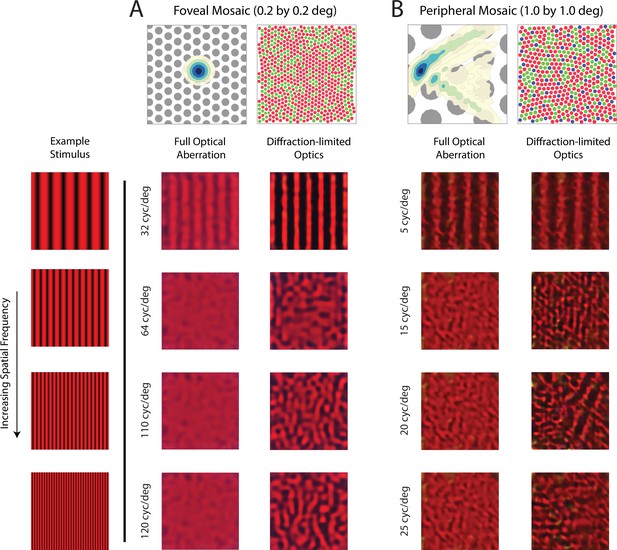
Reconstruction of chromatic grating stimuli with/without optical aberrations.
Image reconstruction of chromatic grating stimuli with increasing spatial frequency from (A) a 0.2 deg foveal mosaic and (B) a 1 deg peripheral mosaic at (18, 18) degrees retinal eccentricity with full optical aberrations (left columns) and with diffraction-limited optics (right columns). The top left images show a contour plot of the point-spread function relative to an expanded view of the cone mosaic, while the top right images show the full mosaic. Images were modulations of the red channel of the simulated monitor, to mimic the 633 nm laser used in the interferometric experiments. The exact frequency of the stimuli being used for each condition is as denoted in the figure. Note that the mottle observed in the reconstructions with full optical aberrations at high spatial frequencies match the reconstruction of a uniform field of saturated red stimulus.
Figure 9—figure supplement 2
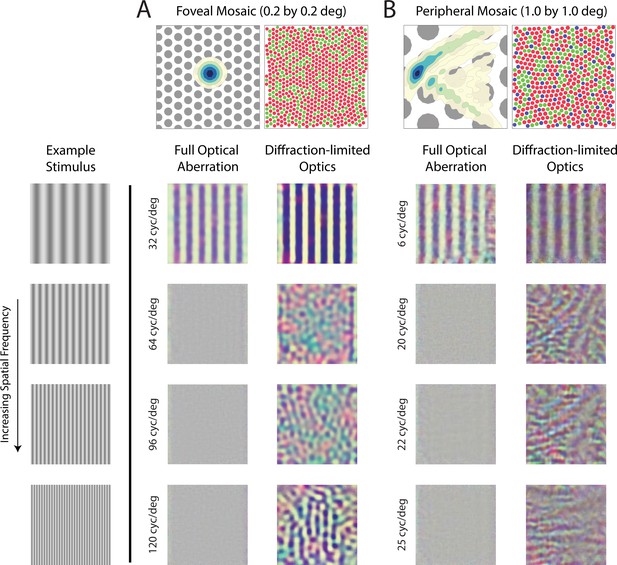
Reconstruction of achromatic grating stimuli with/without optical aberrations.
Image reconstructions of achromatic grating stimuli with increasing spatial frequency from (A) a 0.2 deg foveal mosaic and (B) a 1 deg peripheral mosaic at (18, 18) degree retinal eccentricity with full optical aberration (left columns) and with diffraction-limited optics (right columns). The top left images show a contour plot of the point-spread function relative to an expanded view of the cone mosaic, while the top right images show the full mosaic. The exact frequency of the stimuli being used for each condition is as denoted in the figure. The reconstruction shows similar spatial aliasing as in Figure 9 and Figure 9—figure supplement 1, but shows an additional pattern of chromatic aliasing that arises because of the interleaved sampling by a mosaic of different cone types (Williams et al., 1991; Brainard et al., 2008). Whether such chromatic aliasing would actually be observed if a subject viewed achromatic gratings under diffraction-limited conditions is to our knowledge, an open question.
Figure 10 with 1 supplement
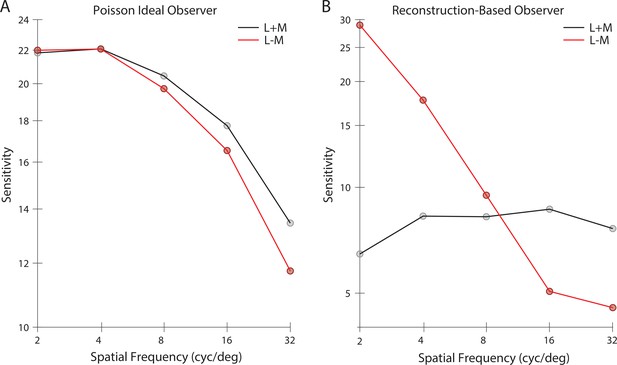
Contrast sensitivity functions.
Contrast sensitivity, defined as the inverse of threshold contrast, for (A) a Poisson 2AFC ideal observer, and (B) an image reconstruction-based observer (see Materials and methods), as a function of the spatial frequency of stimulus in either the L + M direction (black) and L - M cone contrast direction (red). Contrast was measured as the vector length of the cone contrast vector, which is matched across the two color directions.
Figure 10—figure supplement 1
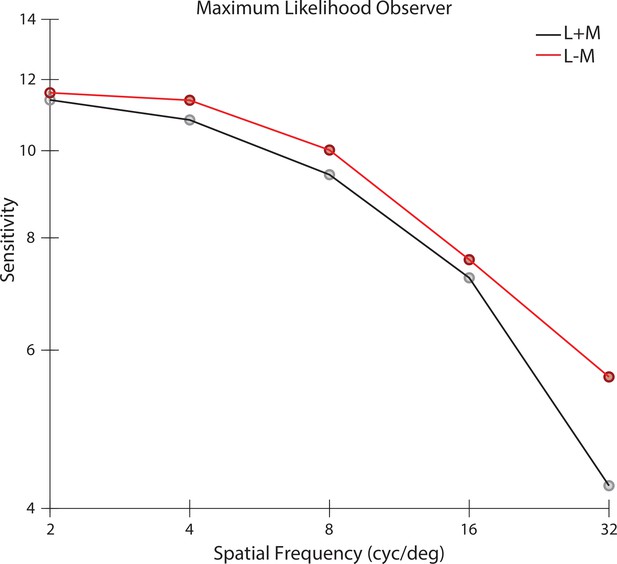
Contrast sensitivity function of a MLE reconstruction observer.
Contrast sensitivity, defined as the inverse of threshold contrast, for an image reconstruction-based observer without the prior term () as a function of the spatial frequency of stimulus in either L + M direction (black) and L - M direction (red) with equal RMS cone contrast. Note that the MLE reconstructions are not unique (see Figure 3). In the computations whose results are shown here, the MLE reconstructions were chosen arbitrarily as the ones converged upon by our particular numerical search algorithm.
Author response image 1
A set of six images with the same (maximum) likelihood for a deuteranopic cone mosaic.
The top-left image is the original image, the bottom-right image is one MLE estimate for the dichromatic mosaic (without cone noise), and the other four images are produced as linear mixtures of the two, with the mixture weights summing to one. Without an explicit prior constraint, all these 6 images (and many others with pixel differences in the null space of the render matrix) provide a valid MLE solution to the reconstruction problem.
Author response image 2
Grayscale image reconstruction from a normal trichromatic mosaic at twilight level, given two different prior weights.
Compare to Figure 7 and Figure 7-S1 in the main text, we did not find meaningful improvements in the quality of the reconstructed images.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
An image reconstruction framework for characterizing initial visual encoding
eLife 11:e71132.
https://doi.org/10.7554/eLife.71132
