Figures and data in Putting the theory into ‘burstlet theory’ with a biophysical model of burstlets and bursts in the respiratory preBötzinger complex

Figures
Tables
Additional files

8 figures, 3 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

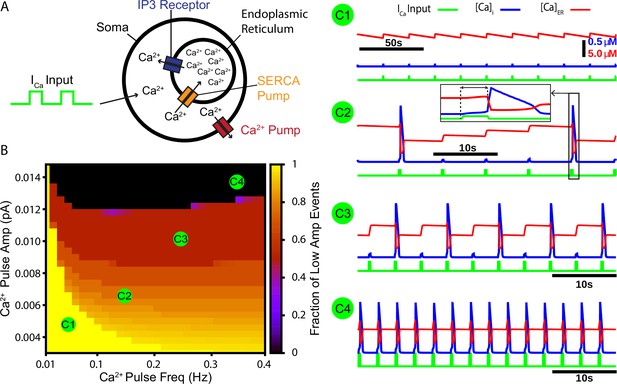
A periodic input in the form of a calcium current drives intermittent calcium-induced calcium release (CICR) from endoplasmic reticulum (ER) stores.

(A) Schematic diagram of the model setup showing square wave profile of Ca²⁺ current input into the intracellular space, uptake of Ca²⁺ into the ER by the sarcoendoplasmic reticulum calcium transport ATPase (SERCA) pump, Ca²⁺ release through the IP3 receptor, and extrusion of Ca²⁺ through a pump in the cell membrane. (B) Fraction of low-amplitude intracellular Ca²⁺ transients as a function of the Ca²⁺ pulse frequency and amplitude. Pulse duration was fixed at 250 ms. (**C1–C4**) Example traces showing several ratios of low- and high-amplitude Ca²⁺ transients and the dynamics of the ER stores Ca²⁺ concentration. Inset in C2 highlights the delay between pulse onset and CICR. The pulse amplitude and frequency for each trace are indicated in panel (B).

Figure 1—source data 1 Calcium-induced calcium release.: https://cdn.elifesciences.org/articles/75713/elife-75713-fig1-data1-v2.xlsx
Download elife-75713-fig1-data1-v2.xlsx

Figure 2 with 1 supplement

Download asset Open asset

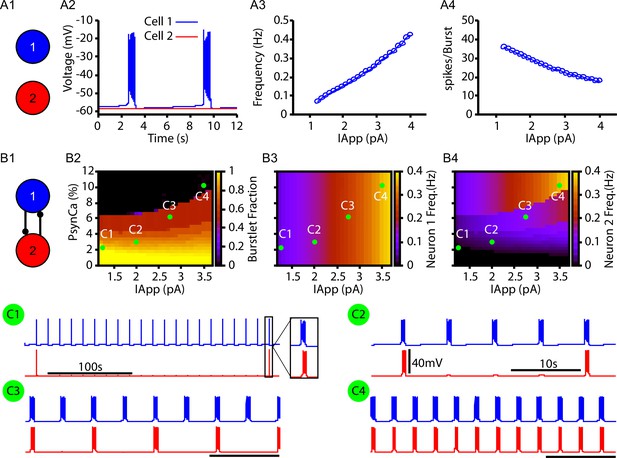
Bursts and burstlets in a two-neuron preBötzinger complex (preBötC) network.

(A1) Schematic diagram of the synaptically uncoupled network. The rhythm- and pattern-generating components of the network are represented by neurons 1 and 2, respectively. (A2) Example trace showing intrinsic bursting in neuron 1 and quiescence in neuron 2. (A3) Burst frequency and (A4) the number of spikes per burst in neuron 1 as a function of an applied current ( $I_{A P P}$ ). Neuron 2 remained quiescent within this range of $I_{A P P}$ . (B1) Schematic diagram of the synaptically coupled network. (**B2–B4**) 2D plots characterizing the (B2) burstlet fraction, (B3) neuron 2 (burst) frequency, and (B4) neuron 2 spikes per burst (burst amplitude) as a function of $I_{A P P}$ and $P_{S y n C a}$ . (**C1–C4**) Example traces for neurons 1 and 2 for various $I_{A P P}$ and $P_{S y n C a}$ values indicated in (**B2–B4**). Notice the scale bar is 100s in C1 and 10s in (**C2–C4**). Inset in (C1) shows the burst shape not visible on the 100 s timescale. The model parameters used in these simulations are: (neurons 1 and 2) $K_{B a t h} = 8 m M$ , $g_{L e a k} = 3.35 n S$ , $W_{12} = W_{21} = 0.006 n S$ ; (neuron 1) $g_{N a P} = 3.33 n S$ , $g_{C A N} = 0.0 n S$ , (neuron 2) $g_{N a P} = 1.5 n S$ , $g_{C A N} = 1.5 n S$ .

Figure 2—source data 1 Burstlets and bursts in a two-neuron network.: https://cdn.elifesciences.org/articles/75713/elife-75713-fig2-data1-v2.xlsx
Download elife-75713-fig2-data1-v2.xlsx

Figure 2—figure supplement 1

Download asset Open asset

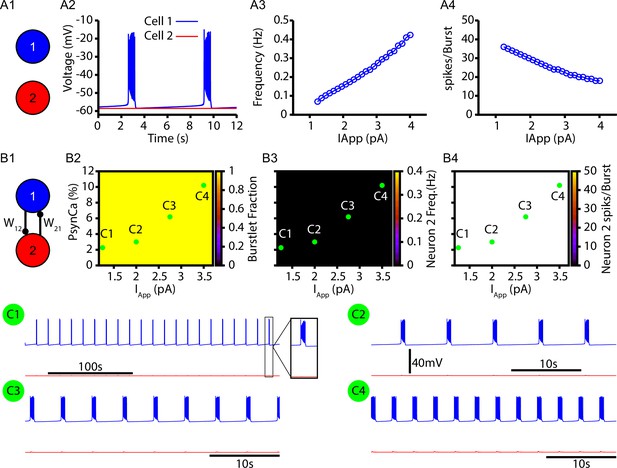
Without calcium-induced calcium release (CICR), the two-neuron network fails to generate bursts (recruitment of neuron 2).

These simulations are identical to those in Figure 2 except the conductance of the IP3 receptor is set to zero ( $G_{I P 3} = 0 / m s$ ). (A1) Schematic diagram of the synaptically uncoupled network. The rhythm- and pattern-generating components of the network are represented by neurons 1 and 2, respectively. (A2) Example trace showing intrinsic bursting in neuron 1 and quiescence in neuron 2. (A3) Burst frequency and (A4) the number of spikes per burst in neuron 1 as a function of an applied current ( $I_{A P P}$ ). Neuron 2 remained quiescent within this range of $I_{A P P}$ . (B1) Schematic diagram of the synaptically coupled network. (**B2–B4**) 2D plots characterizing the (B2) burstlet fraction, (B3) neuron 2 (burst) frequency, and (B4) neuron 2 spikes per burst (burst amplitude) as a function of $I_{A P P}$ and $P_{S y n C a}$ . (**C1–C4**) Example traces for neurons 1 and 2 for various $I_{A P P}$ and $P_{S y n C a}$ values indicated in (**B2–B4**). Notice that neuron 2 is never recruited by the bursting in neuron 1 for any of the conditions tested. The model parameters used in these simulations are: (neurons 1 and 2) $K_{B a t h} = 8 m M$ , $g_{L e a k} = 3.35 n S$ , $W_{12} = W_{21} = 0.006 n S$ ; (neuron 1) $g_{N a P} = 3.33 n S$ , $g_{C A N} = 0.0 n S$ , (neuron 2) $g_{N a P} = 1.5 n S$ , $g_{C A N} = 1.5 n S$ .

Figure 3 with 1 supplement

Download asset Open asset

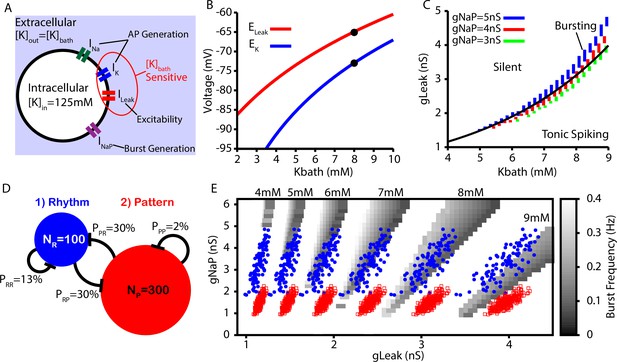
Intrinsic cellular and network dynamics depend on the bath potassium concentration.

(A) Schematic diagram of an isolated model preBötzinger complex (preBötC) neuron showing the simulated ion channels involved in AP generation, excitability, and burst generation, as well as indication of currents directly affected by changing the bath potassium concentration ( $K_{b a t h}$ ). (B) Dependence of potassium ( $E_{K}$ ) and leak ( $E_{L e a k}$ ) reversal potentials on $K_{b a t h}$ . Black dots indicate experimentally measured values for $E_{K}$ and $E_{L e a k}$ from Koizumi and Smith, 2008. (C) Dependence of intrinsic cellular dynamics on $K_{b a t h}$ , $g_{L e a k}$ , and $g_{N a P}$ . Black curve represents the relationship between $K_{B a t h}$ and $g_{L e a k}$ used in the full preBötC network. (D) Schematic diagram of size and connectivity probabilities of the rhythm- and pattern-generating populations within the preBötC model. (E) 2D plot between $g_{N a P}$ and $g_{L e a k}$ showing the location of the intrinsic bursting regime for varied concentrations of $K_{B a t h}$ . The distributions of neuronal conductances in the rhythm- and the pattern-generating populations are indicated by the blue dots and red squares, respectively.

Figure 3—source data 1 Bath potassium concentration dependence of cellular and network dynamics.: https://cdn.elifesciences.org/articles/75713/elife-75713-fig3-data1-v2.xlsx
Download elife-75713-fig3-data1-v2.xlsx

Figure 3—figure supplement 1

Download asset Open asset

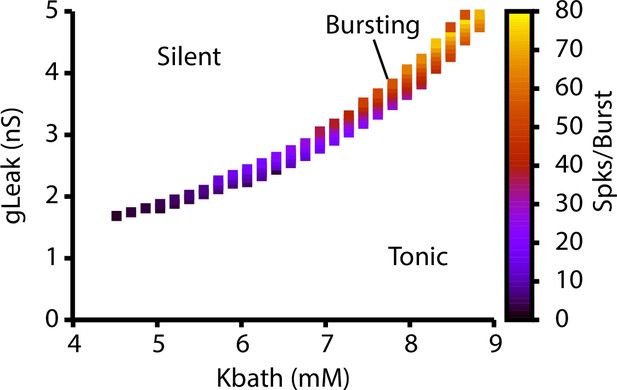
Dependence of intrinsic cellular dynamics and the number of spikes per burst on $K_{b a t h}$ and $g_{L e a k}$ .

For these simulations, $g_{N a P} = 5.0 n S$ .

Figure 4 with 1 supplement

Download asset Open asset

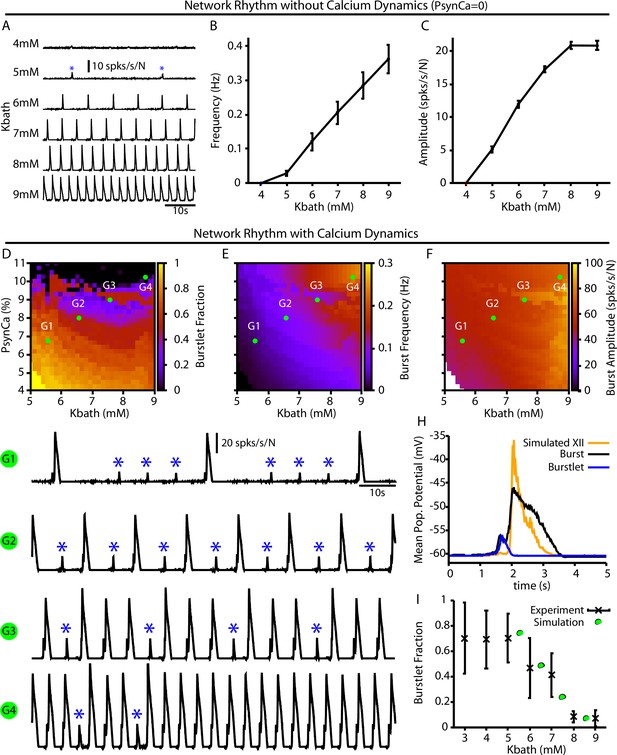
Burstlets and bursts in a 400-neuron preBötzinger complex (preBötC) network model with and without calcium dynamics.

(A) Rhythmogenic output of the simulated network without calcium dynamics ( $P_{S y n C a} = 0$ ) as a function of $K_{B a t h}$ . These oscillations are considered burstlets as they are incapable of recruiting the pattern-generating population without calcium dynamics. (B) Frequency and (C) amplitude of the burstlet oscillations as a function of $K_{b a t h}$ . (**D–F**) 2D plots characterizing the (D) burstlet fraction, (E) the burst frequency, and (F) the burst amplitude as a function of $K_{b a t h}$ and $P_{S y n C a}$ (note that the $P_{S y n C a}$ range shown does not start at 0). (**G1–G4**) Example traces illustrating a range of possible burstlet fractions generated by the network. Burstlets are indicated by asterisks. (H) Overlay of the average population voltage during bursts and burstlets. The hypoglossal output is calculated by passing the mean population amplitude through a sigmoid function $f = - 60.5 + 60 / [1 + e^{- (x + 45) / 2.5}]$ . (I) Burstlet fraction as a function of $K_{b a t h}$ for the four example traces indicated in panels (**G1–G4**). Figure 4I has been adapted from Figure 1B from Kallurkar et al., 2020.

Figure 4—source data 1 Burstlets and Bursts in a larger network.: https://cdn.elifesciences.org/articles/75713/elife-75713-fig4-data1-v2.xlsx
Download elife-75713-fig4-data1-v2.xlsx

Figure 4—figure supplement 1

Download asset Open asset

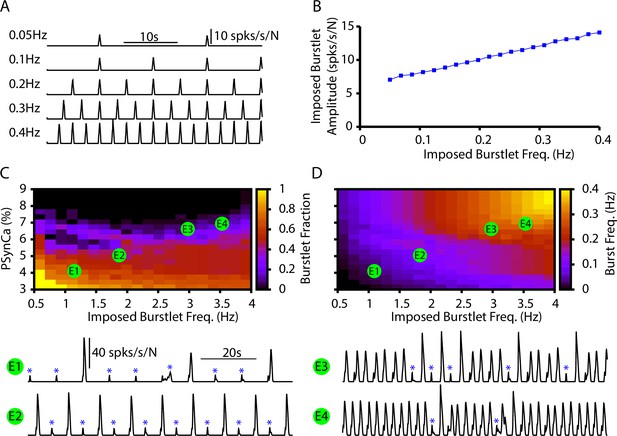
Burstlets and bursts in a 400-neuron preBötzinger complex (preBötC) network model with an imposed burstlet rhythm.

(A) Example traces of the imposed burstlet rhythm where $P_{S y n C a} = 0$ so that the pattern-generating population is not recruited. (B) Dependence of the burstlet amplitude on frequency. The burstlet frequency range and doubling of the burstlet amplitude were chosen to qualitatively match the effects of changing $K_{b a t h}$ on burstlet properties characterized in Kallurkar et al., 2020. (**C, D**) 2D plots characterizing the (C) burstlet fraction and (D) the burst frequency as a function of the burstlet frequency and $P_{S y n C a}$ (note that the $P_{S y n C a}$ range shown does not start at 0). (**E1–E4**) Example traces illustrating a range of possible burstlet fractions generated by the network. Burstlets are indicated by asterisks. The imposed burstlet rhythm was generated by imposing a Poisson spike train in each neuron within the rhythmogenic population where the frequency was zero during the interburst interval. At the start of the burstlet, the frequency linearly ramps up over 250 ms to an imposed maximum firing rate and then linearly ramps back down to zero over an additional 250 mS. The burstlet frequency and amplitude were controlled by changing the interburst interval and the maximum firing rate, respectively.

Figure 5

Download asset Open asset

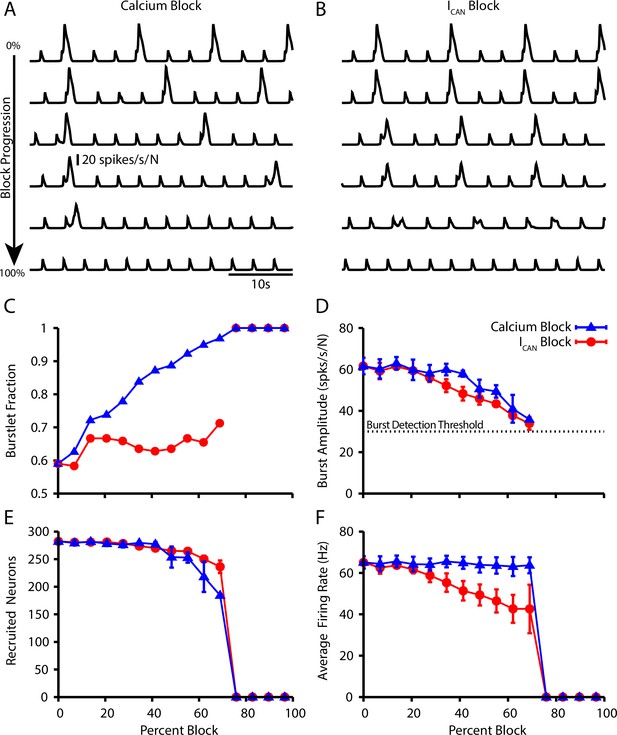
Effect of Ca²⁺ and CAN current blockade on burstlets and bursts.

Network traces showing the effect of (A) calcium current blockade ( $P_{S y n C a}$ reduction) and (B) CAN current blockade ( $g_{C A N}$ reduction) on the period and amplitude of bursts. Effects of calcium or $I_{C A N}$ blockade on (C) the burstlet fraction, (D) the amplitude of bursts and (E) the number of recruited and (F) peak firing rate of recruited neurons in pattern-generating subpopulation during network bursts as a function of the blockade percentage.

Figure 5—source data 1 Simulated calcium or CAN current blockade.: https://cdn.elifesciences.org/articles/75713/elife-75713-fig5-data1-v2.xlsx
Download elife-75713-fig5-data1-v2.xlsx

Figure 6

Download asset Open asset

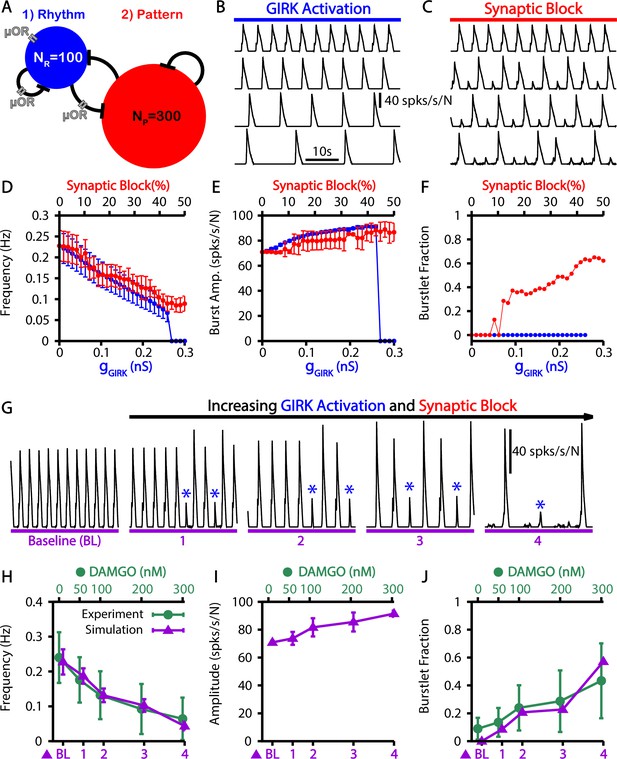
Simulated μ-opioid receptor (μOR) activation by local DAMGO application in the preBötzinger complex (preBötC) and comparison with experimental data.

(A) Schematic preBötC network diagram showing the location of μOR. Example traces showing the effect of progressive (from top to bottom) (B) $g_{G I R K}$ channel activation and (C) synaptic block on the network output. Quantification of $g_{G I R K}$ activation or synaptic block by μOR on the (D) burst frequency, (E) burst amplitude, and (F) burstlet fraction. Error bars indicate SD. (G) Example traces showing the effects of progressive increases in $g_{G I R K}$ and synaptic block on network output. Burstlets are indicated by blue asterisks. The parameters for each case are as follows: (BL) $g_{G I R K} = 0.0 n S$ , $γ_{μ O R} = 0.0$ ; (1) $g_{G I R K} = 0.031034 n S$ , $γ_{μ O R} = 0.81034$ ; (2) $g_{G I R K} = 0.093103 n S$ , $γ_{μ O R} = 0.7069$ ; (3) $g_{G I R K} = 0.14483 n S$ , $γ_{μ O R} = 0.68966$ ; (4) $g_{G I R K} = 0.19655 n S$ , $γ_{μ O R} = 0.58621$ . Comparison of experimental data and the effects of progressive increases in $g_{G I R K}$ and synaptic block on the (H) frequency and (I) amplitude of bursts as well as (J) the burstlet fractions for the traces shown in (G). Figure 6H and J have been adapted from Figure 3C and E from Baertsch et al., 2021. The effects of DAMGO on burst amplitude were not quantified in Baertsch et al., 2021.

Figure 6—source data 1 Effects of simulated opioids on burstlets and bursts.: https://cdn.elifesciences.org/articles/75713/elife-75713-fig6-data1-v2.xlsx
Download elife-75713-fig6-data1-v2.xlsx

Figure 7 with 1 supplement

Download asset Open asset

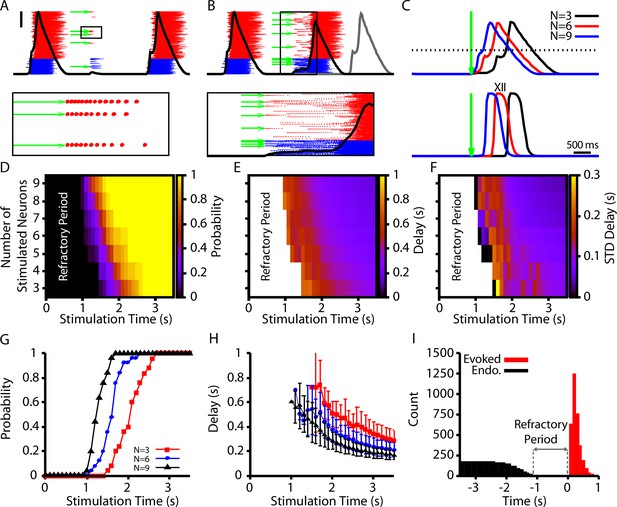
Evoked population bursts by simulated holographic stimulation of 3–9 preBötzinger complex (preBötC) neurons.

(A) Raster plot of neuronal spiking triggered by simulated holographic stimulation of six preBötC neurons shortly after an endogenous burst and resulting failure to evoke a network burst. Black line represents the integrated population activity. Scale bar indicates 20 spikes/s/N. Bottom panel shows the spiking activity triggered in individual neurons by the simulated holographic stimulation. Panel duration is 1 s. (B) Example simulation where stimulation of nine preBötC neurons evokes a network burst. Gray curve indicates timing of the next network burst if the network was not stimulated. (Bottom panel) Expanded view of the percolation process that is triggered by holographic stimulation on a successful trial. Panel duration is 1.75 s. (C) Example traces showing the delay between the stimulation time and the evoked bursts as a function of the number of neurons stimulated for the (top) integrated preBötC spiking and (bottom) simulated hypoglossal activity. (**D–F**) Characterization of (D) the probability of evoking a burst, (E) the mean delay of evoked bursts, and (F) the standard deviation of the delay as a function of the time after an endogenous burst and the number of neurons stimulated. (G) Probability and (H) delay as a function of the stimulation time for stimulation of three, six, or nine neurons. Error bars in (H) indicate SD. (I) Histogram of evoked and endogenous bursts relative to the time of stimulation ( $t = 0 s)$ for all successful trials in all simulations; notice a 1 s refractory period.

Figure 7—source data 1 Simulated holographic stimulation.: https://cdn.elifesciences.org/articles/75713/elife-75713-fig7-data1-v2.xlsx
Download elife-75713-fig7-data1-v2.xlsx

Figure 7—figure supplement 1

Download asset Open asset

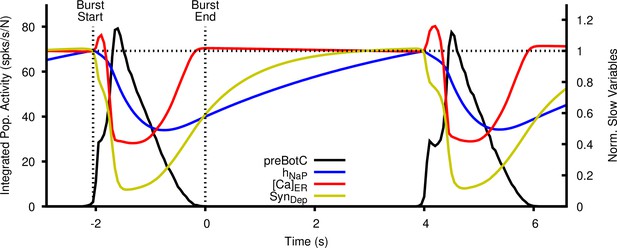
Dynamics of $I_{N a P}$ inactivation ( $h_{N a P}$ ), endoplasmic reticulum (ER) calcium concentration ( ${[C a]}_{E R}$ ), and synaptic depression and recovery ( $D$ ) as a function of time relative to the inspiratory cycle.

The values of $h_{N a P}$ , ${[C a]}_{E R}$ and $D$ are normalized to their values at the start of the burst.

Figure 8

Download asset Open asset

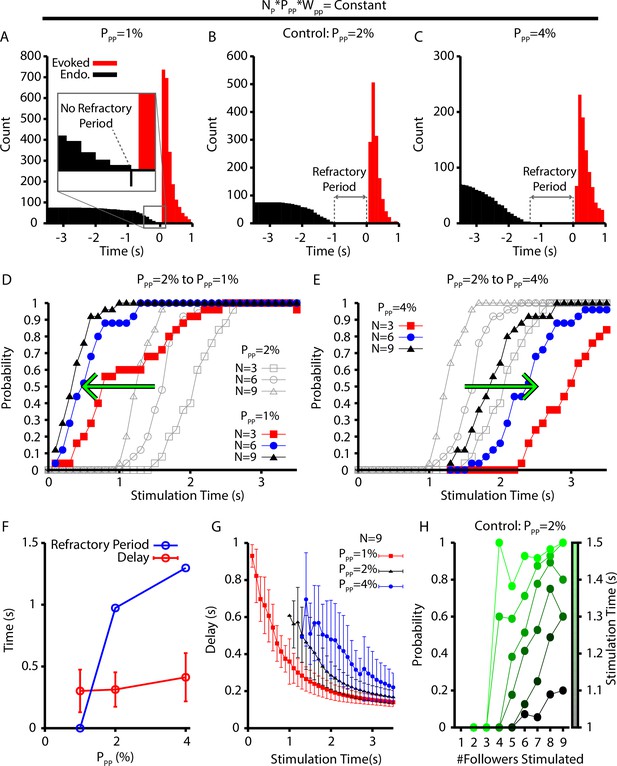
Refractory period and delay of evoked bursts following simulated holographic stimulation depend on the follower network connectivity.

(**A–C**) Histogram of evoked and endogenous bursts relative to the time of stimulation ( $t = 0 s)$ for all successful trials where three, six, and nine neurons were stimulated and for different connection probabilities (but fixed total network synaptic strength; i.e., $N_{P} \cdot P_{P P} \cdot W_{P P} = c o n s t a n t$ ) in the follower population: (A) $P_{P P} = 1 %$ ; (B) $P_{P P} = 2 %$ ; and (C) $P_{P P} = 4 %$ . (**D, E**) Effect of (D) decreasing ( $2 % \to 1 %$ ) and (E) increasing ( $2 % \to 4 %$ ) the connection probability in the follower population, $P_{P P}$ . (F) Refractory period and delay from stimulation to burst as functions of the connection probability for the simulations shown in (**A–E**), still with $N_{P} \cdot P_{P P} \cdot W_{P P} = c o n s t a n t$ . Error bars indicate SD. Notice that the refractory period increases with increasing connection probability. (G) Effect of $P_{P P}$ on the delay to evoked bursts. (H) Probability of evoking a burst as a function of time of stimulation delivery (colorbar) and the number out of nine stimulated neurons that are follower neurons for the baseline case of 2% connection probability.

Figure 8—source data 1 Refractory period of evoked bursts following holographic stimulation.: https://cdn.elifesciences.org/articles/75713/elife-75713-fig8-data1-v2.xlsx
Download elife-75713-fig8-data1-v2.xlsx

Tables

Table 1

Ionic channel parameters.

Channel	Parameters
$I_{N a}$	$g_{N a} = 150 n S$	$E_{N a} = 26.54 \cdot l n (N a_{o u t} / N a_{i n})$	$N a_{i n} = 15 m M$	$N a_{o u t} = 120 m M$
	$m_{1 / 2} = - 43.8 m V$	$k_{m} = 6.0 m V$	$τ_{m a x}^{m} = 0.25 m s$	$τ_{1 / 2}^{m} = - 43.8 m V$	$k_{τ}^{m} = 14.0 m V$
	$h_{1 / 2} = - 67.5 m V$	$k_{h} = - 11.8 m V$	$τ_{m a x}^{h} = 8.46 m s$	$τ_{1 / 2}^{h} = - 67.5 m V$	$k_{τ}^{h} = 12.8 m V$
$I_{K}$	$g_{K} = 220 n S$	$E_{K} = 26.54 \cdot l n (K_{b a t h} / K_{i n})$	$K_{i n} = 125$	$K_{B a t h} = V A R$
	$A_{α} = 0.011$	$B_{α} = 44.0 m V$	$k_{α} = 5.0 m V$
	$A_{β} = 0.17$	$B_{β} = 49.0 m V$	$k_{β} = 40.0 m V$
$I_{N a P}$	$g_{N a P} = N (μ, σ)$ , see Table 2
	$m_{1 / 2} = - 47.1 m V$	$k_{m} = 3.1 m V$	$τ_{m a x}^{m} = 1.0 m s$	$τ_{1 / 2}^{m} = - 47.1 m V$	$k_{τ}^{m} = 6.2 m V$
	$h_{1 / 2} = - 60.0 m V$	$k_{h} = - 9.0 m V$	$τ_{m a x}^{h} = 5000 m s$	$τ_{1 / 2}^{h} = - 60.0 m V$	$k_{τ}^{h} = 9.0 m V$
$I_{C a}$	$g_{C a} = 0.0065 p S$	$E_{C a} = 13.27 \cdot l n (C a_{o u t} / C a_{i n})$		$C a_{o u t} = 4.0 m M$
	$m_{1 / 2} = - 27.5 m V$	$k_{m} = 5.7 m V$	$τ_{m} = 0.5 m s$
	$h_{1 / 2} = - 52.4 m V$	$k_{h} = - 5.2 m V$	$τ_{h} = 18.0 m s$
$I_{C A N}$	$g_{C A N} = N (μ, σ)$ , see Table 2	$E_{C A N} = 0.0 m V$	$C a_{1 / 2} = 0.00074 m M$	$n = 0.97$
$I_{L e a k}$	$g_{L e a k} = N (μ, σ)$ , see Table 2	$E_{L e a k} = - 26.54 * l n [(P_{N a} * N a_{i n} + P_{K} * K_{i n}) / (P_{N a} * N a_{o u t} + P_{K} * K_{b a t h})]$
	$P_{N a} = 1$	$P_{K} = 42$
$I_{S y n}$	$g_{S y n} = V A R$ , see Equation 25	$E_{S y n} = 0.0 m V$	$τ_{S y n} = 5.0 m s$
$I_{G I R K}$	$g_{G I R K} = 0 - 0.3 n S$	$E_{G I R K} = E_{K}$
$I_{H o l o}$	$g_{H o l o} = 50 n S$	$τ_{H o l o} = 100 m s$	$E_{H o l o} = E_{S y n}$

Table 2

Distributed channel conductances.

Type	$g_{N a P} (n S)$		$g_{L e a k} (n S)$		$g_{C A N} (n S)$
Type	μ	σ	μ	σ	μ	σ
Rhythm	3.33	0.75	$e x p ((K_{B a t h} - 3.425) / 4.05)$	$0.05 \cdot μ_{l e a k}$	0.0	0.0
Pattern	1.5	0.25	$e x p ((K_{B a t h} - 3.425) / 4.05)$	$0.025 \cdot μ_{l e a k}$	2.0	1.0

Table 3

Maximal synaptic weights and connection probabilities between and within rhythm- and pattern-generating preBötC subpopulations ( $W_{M a x}, P$ ).

		Target
		Rhythm	Pattern
Source	Rhythm	(0.15 nS, 0.13)	(0.000175 nS, 0.3)
Source	Pattern	(0.25 nS, 0.3)	(0.0063 nS, 0.02)

Additional files

Transparent reporting form: https://cdn.elifesciences.org/articles/75713/elife-75713-transrepform1-v2.docx
Download elife-75713-transrepform1-v2.docx

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Ryan S Phillips
Jonathan E Rubin

(2022)

Putting the theory into ‘burstlet theory’ with a biophysical model of burstlets and bursts in the respiratory preBötzinger complex

eLife 11:e75713.

https://doi.org/10.7554/eLife.75713

Share this article

Cite this article

A periodic input in the form of a calcium current drives intermittent calcium-induced calcium release (CICR) from endoplasmic reticulum (ER) stores.

Figure 1—source data 1

Bursts and burstlets in a two-neuron preBötzinger complex (preBötC) network.

Figure 2—source data 1

Without calcium-induced calcium release (CICR), the two-neuron network fails to generate bursts (recruitment of neuron 2).

Intrinsic cellular and network dynamics depend on the bath potassium concentration.

Figure 3—source data 1

Dependence of intrinsic cellular dynamics and the number of spikes per burst on Kb⁢a⁢t⁢h and gL⁢e⁢a⁢k.

Burstlets and bursts in a 400-neuron preBötzinger complex (preBötC) network model with and without calcium dynamics.

Figure 4—source data 1

Burstlets and bursts in a 400-neuron preBötzinger complex (preBötC) network model with an imposed burstlet rhythm.

Effect of Ca2+ and CAN current blockade on burstlets and bursts.

Figure 5—source data 1

Simulated μ-opioid receptor (μOR) activation by local DAMGO application in the preBötzinger complex (preBötC) and comparison with experimental data.

Figure 6—source data 1

Evoked population bursts by simulated holographic stimulation of 3–9 preBötzinger complex (preBötC) neurons.

Figure 7—source data 1

Dynamics of IN⁢a⁢P inactivation (hN⁢a⁢P), endoplasmic reticulum (ER) calcium concentration ([C⁢a]E⁢R), and synaptic depression and recovery (D) as a function of time relative to the inspiratory cycle.

Refractory period and delay of evoked bursts following simulated holographic stimulation depend on the follower network connectivity.

Figure 8—source data 1

Ionic channel parameters.

Distributed channel conductances.

Maximal synaptic weights and connection probabilities between and within rhythm- and pattern-generating preBötC subpopulations (WM⁢a⁢x,P).

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Dependence of intrinsic cellular dynamics and the number of spikes per burst on $K_{b a t h}$ and $g_{L e a k}$ .

Effect of Ca²⁺ and CAN current blockade on burstlets and bursts.

Dynamics of $I_{N a P}$ inactivation ( $h_{N a P}$ ), endoplasmic reticulum (ER) calcium concentration ( ${[C a]}_{E R}$ ), and synaptic depression and recovery ( $D$ ) as a function of time relative to the inspiratory cycle.

Maximal synaptic weights and connection probabilities between and within rhythm- and pattern-generating preBötC subpopulations ( $W_{M a x}, P$ ).