Vasculature: Exploring the dynamics of vascular adaptation
A combination of in toto imaging and theory suggests a new mechanism for the remodeling of veins in vascular networks.
- AMOLF, Netherlands
- Amsterdam Institute for Life and Environment, Vrije Universiteit Amsterdam, Netherlands
- Department of Mechanical and Aerospace Engineering, Princeton University, United States
Many processes in biology rely on molecules and other objects moving from A to B. These movements are dominated by diffusion at the smallest scales (Berg, 1993), but diffusion is prohibitively slow for distances greater than a few millimeters, so nature relies on the directed flow of fluids instead. The best-known example of this is the use of blood to transport nutrients, gases and waste materials around the body (Wootton and Ku, 1999). However, vascular networks have evolved many times across diverse domains of life: even microbes such as bacteria (Claessen et al., 2014; Wilking et al., 2013) and fungi (Fricker et al., 2017b; Whiteside et al., 2019) are known to build fluid flow networks for the long-range transport of nutrients and other substances within colonies. Given the importance of vascular networks for so many organisms, a natural question arises: what are the unifying principles, if any, that govern the design of such networks?
One possible answer to this question was proposed by Cecil D Murray of Bryn Mawr College nearly a century ago (Murray, 1926). By considering the energetic costs of pressure-driven blood flow, Murray identified a simple relationship between three physical parameters (the radius of the blood vessel, a; the flow rate, Q; and the viscosity of blood, µ), and a single physiological parameter (the rate of energy dissipation required to maintain a vein, per unit volume, b). This relationship – now known as Murray’s law – can be written as: a6=16µQ2/π2b.
Since then, various predictions that follow from Murray’s law have been shown to hold for a range of vascular networks in animals (West et al., 1997), plants (McCulloh et al., 2003) and microbes (such as the slime mold Physarum polycephalum; Fricker et al., 2017a). However, Murray’s law only applies to flow networks that do not change with time, and it does not address how such networks are built in the first place, or how they remodel themselves in response to anatomical and/or physiological changes. A lack of high-quality data on vascular flows and morphology at the scale of the entire network has hindered efforts to understand how vascular networks grow and remodel themselves over time.
Now, in eLife, Karen Alim (Technical University of Munich) and co-workers – including Sophie Marbach (New York University) and Noah Ziethen (Max Planck Institute for Dynamics and Self-Organization) as joint first authors, Leonie Bastin and Felix Bäuerle – report the results of extensive experimental and theoretical work to understand how the vascular networks formed by P. polycephalum change over time (Marbach et al., 2023b).
Combining high-resolution measurements of flow inside individual veins with time-lapse imaging of entire networks (Figure 1), Marbach et al. first discovered that the radius of a vein changes when the local shear rate of the fluid flow changes, albeit with a time delay. The researchers then plotted the trajectories of individual veins in a “phase space” with vein radius as the x-axis and shear rate as the y-axis. This revealed a rich repertoire of dynamical behaviors, such as oscillating orbits and runaway decays. Moreover, these behaviors could be classified into several categories, depending on the eventual fate of the vein (e.g., some veins were stable and supported contractile oscillations, whereas others were unstable and shrunk to extinction) and other factors. Such rich dynamics cannot be explained by Murray’s law, which predicts only a fixed relationship between the shear rate and vein radius.
Figure 1
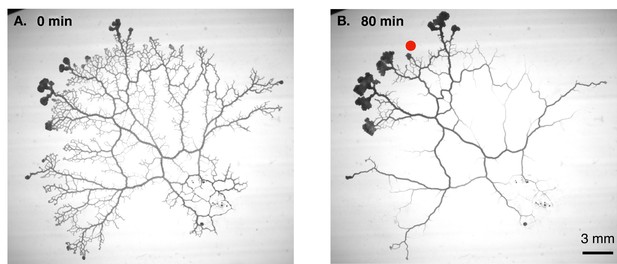
Vascular remodelling observed in real time.
(A) Image showing the vascular network formed by the slime mould Physarum polycephalum. (B) Image of the same network 80 minutes later. Note that many veins have disappeared, whereas others have maintained a constant thickness, and some have become thicker. The new vascular adaptation model developed by Marbach et al. can predict these contrasting fates for individual veins in the network. Red dot shows veins where shear rate is initially low.
Marbach et al. then developed a detailed mathematical framework that consisted of three parts: (i) a model of how the vein radius responds to changes in the shear rate that takes into account the observed time delay and force balance in wall of the vein; (ii) a model of fluid flows in contractile veins; (iii) a method to extract certain network parameters that are required to apply the vein adaptation model (i) and the flow model (ii) to experimental data. The method used to extract these parameters – which reflect the global topology and morphology of the network – involved the application of Kirchoff’s circuit laws to fluid flow networks.
A key ingredient of the new model is a mechanism for sensing the local shear rate. This mechanism relies on a peculiar feature of the actin cytoskeletal networks that drive the contractile dynamics of veins in P. polycephalum (Isenberg and Wohlfarth-Bottermann, 1976). Specifically, it has been shown that networks of semi-flexible polymers such as actin can contract in response to shear stresses, in a direction that is, counter-intuitively, orthogonal to the direction of the applied shear (Janmey et al., 2007). The researchers argue that this property of actin can provide a mechanism that enables local shear (due to fluid flow along the long axis of a vein) to lead to an increase in the radius of the vein (see the accompanying preprint; Marbach et al., 2023a).
Through extensive mathematical analyses, Marbach et al. succeeded in reducing these detailed considerations to an elegant model consisting of just three equations: one describing the shear-rate feedback (via the actin cytoskeleton), a second describing the observed time delay at a phenomenological level, and a third describing the dependence of local shear rate on the global architecture of the network. Despite its simplicity, when calibrated by flow-resistance calculations based on morphological data for the full network, this model faithfully reproduced the rich set of dynamics observed for individual veins over time, including their eventual fate – that is, whether they are stable and oscillate about a fixed point (with this point being predicted by Murray’s law), or are unstable and shrink to extinction over time.
Crucial for the successful validation and application of the model was the acquisition of high-quality spatial and temporal data on the detailed shape of the P. polycephalum network in toto – that is, across the entirety of the network. It is challenging to collect data of such completeness for vasculature studies in macroscopic organisms. However, advances in the imaging of large volumes (Stephan et al., 2019) and the advent of organoid models of vasculature (Wimmer et al., 2019) raise the exciting prospect that it may soon become possible to test the generality of this new model in other systems.
Equally compelling are the implications of the latest findings in the broader context of organism-scale behavior in natural environments. Given there are ~900 different species of slime molds of various shapes, structure and sizes (Meena et al., 2022), this new model provides a foundation for asking previously unimagined questions about how vascular adaptation dynamics enables, and is in turn affected by, a dynamic networked anatomy that captures and feeds on microbial prey while navigating through ecosystems.
References
-
Bacterial solutions to multicellularity: A tale of Biofilms, filaments and fruiting bodiesNature Reviews Microbiology 12:115–124.https://doi.org/10.1038/nrmicro3178
-
Automated analysis of Physarum network structure and DynamicsJournal of Physics D 50:254005.https://doi.org/10.1088/1361-6463/aa72b9
-
The mycelium as a networkThe Fungal Kingdom 5:335–367.https://doi.org/10.1128/microbiolspec.FUNK-0033-2017
-
Transformation of cytoplasmic actin importance for the organization of the contractile gel reticulum and the contraction—relaxation cycle of cytoplasmic actomyosinCell and Tissue Research 173:495–528.
-
Negative normal stress in semiflexible biopolymer gelsNature Materials 6:48–51.https://doi.org/10.1038/nmat1810
-
BookSlime MoldsIn: Vonk J, Shackelford TK, editors. Encyclopedia of Animal Cognition and Behavior. Springer International Publishing. pp. 6485–6489.https://doi.org/10.1007/978-3-319-55065-7_1334
-
Fluid mechanics of vascular systems, diseases, and thrombosisAnnual Review of Biomedical Engineering 1:299–329.https://doi.org/10.1146/annurev.bioeng.1.1.299
Article and author information
Author details
Publication history
Copyright
© 2023, Shimizu et al.
This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.
Metrics
-
- 871
- views
-
- 94
- downloads
-
- 1
- citations
Views, downloads and citations are aggregated across all versions of this paper published by eLife.
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Vasculature: Exploring the dynamics of vascular adaptation
eLife 12:e88052.
https://doi.org/10.7554/eLife.88052
Further reading
-
- Physics of Living Systems
In social behavior research, the focus often remains on animal dyads, limiting the understanding of complex interactions. Recent trends favor naturalistic setups, offering unique insights into intricate social behaviors. Social behavior stems from chance, individual preferences, and group dynamics, necessitating high-resolution quantitative measurements and statistical modeling. This study leverages the Eco-HAB system, an automated experimental setup that employs radiofrequency identification tracking to observe naturally formed mouse cohorts in a controlled yet naturalistic setting, and uses statistical inference models to decipher rules governing the collective dynamics of groups of 10–15 individuals. Applying maximum entropy models on the coarse-grained co-localization patterns of mice unveils social rules in mouse hordes, quantifying sociability through pairwise interactions within groups, the impact of individual versus social preferences, and the effects of considering interaction structures among three animals instead of two. Reproducing co-localization patterns of individual mice reveals stability over time, with the statistics of the inferred interaction strength capturing social structure. By separating interactions from individual preferences, the study demonstrates that altering neuronal plasticity in the prelimbic cortex – the brain structure crucial for sociability – does not eliminate signatures of social interactions, but makes the transmission of social information between mice more challenging. The study demonstrates how the joint probability distribution of the mice positions can be used to quantify sociability.
-
- Physics of Living Systems
Chromosome structure is complex, and many aspects of chromosome organization are still not understood. Measuring the stiffness of chromosomes offers valuable insight into their structural properties. In this study, we analyzed the stiffness of chromosomes from metaphase I (MI) and metaphase II (MII) oocytes. Our results revealed a tenfold increase in stiffness (Young’s modulus) of MI chromosomes compared to somatic chromosomes. Furthermore, the stiffness of MII chromosomes was found to be lower than that of MI chromosomes. We examined the role of meiosis-specific cohesin complexes in regulating chromosome stiffness. Surprisingly, the stiffness of chromosomes from three meiosis-specific cohesin mutants did not significantly differ from that of wild-type chromosomes, indicating that these cohesins may not be primary determinants of chromosome stiffness. Additionally, our findings revealed an age-related increase of chromosome stiffness for MI oocytes. Since aging is associated with elevated levels of DNA damage, we investigated the impact of etoposide-induced DNA damage on chromosome stiffness and found that it led to a reduction in stiffness in MI oocytes. Overall, our study underscores the dynamic and cyclical nature of chromosome stiffness, modulated by both the cell cycle and age-related factors.
