1. Cancer Biology
  2. Computational and Systems Biology

Quantifying chromosomal instability from intratumoral karyotype diversity using agent-based modeling and Bayesian inference

  1. Andrew R Lynch
  2. Nicholas L Arp
  3. Amber S Zhou
  4. Beth A Weaver
  5. Mark E Burkard  Is a corresponding author
  1. Carbone Cancer Center, University of Wisconsin-Madison, United States
  2. McArdle Laboratory for Cancer Research, University of Wisconsin-Madison, United States
  3. Department of Cell and Regenerative Biology, University of Wisconsin, United States
  4. Division of Hematology Medical Oncology and Palliative Care, Department of Medicine University of Wisconsin, United States
https://doi.org/10.7554/eLife.69799
Share this article
Cite this article
  1. Andrew R Lynch
  2. Nicholas L Arp
  3. Amber S Zhou
  4. Beth A Weaver
  5. Mark E Burkard
(2022)
Quantifying chromosomal instability from intratumoral karyotype diversity using agent-based modeling and Bayesian inference
eLife 11:e69799.
https://doi.org/10.7554/eLife.69799
  2. Download BibTeX
  3. Download .RIS
6 figures, 5 tables and 1 additional file

Figures

Figure 1 with 2 supplements
Download asset Open asset
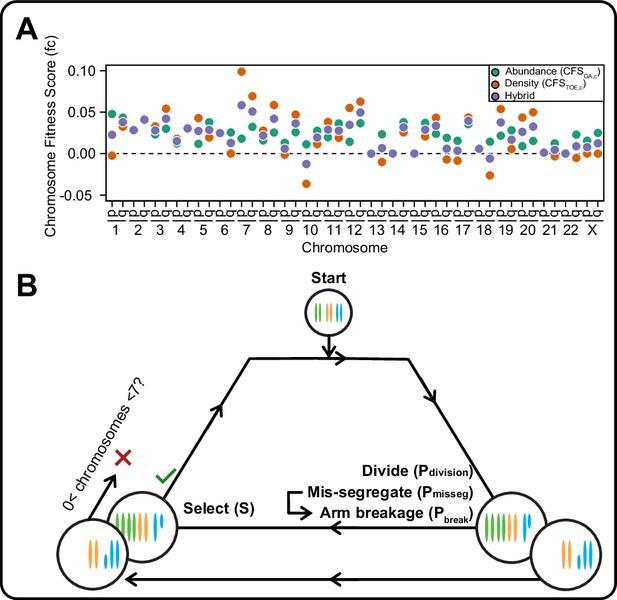
A framework for modeling CIN and karyotype selection.

(A) Chromosome arm scores for each model of karyotype selection. Gene Abundance scores are derived from the number of genes per chromosome arm normalized to the number of all genes. Chromosome arms 13 p and 15 p did not have an abundance score and were set to 0. Driver Density scores come from the pan-cancer chromosome arm scores derived in Davoli et al., 2013, and normalized to the sum of chromosome arm scores for chromosomes 1-22,X. Chromosome arms 13 p, 14 p, 15 p, 21 p, 22 p, and chromosome X did not have driver scores and were set to 0. Hybrid model scores are set to the average of the Driver and Abundance models. The neutral model (not displayed) is performed with all cell’s fitness constitutively equal to 1 regardless of karyotype. (B) Framework for the simulation of and selection on cellular populations with CIN. Cells divide (Pdivision starts at 0.5 in the exponential pseudo-Moran model and is constitutively equal to 1 for the constant Wright-Fisher model) and probabilistically mis-segregate chromosomes (Pmisseg ∈ [0, 0.001… 0.05]). After, cells experience selection under one of the selection models, altering cellular fitness and the probability (Pdivision) a cell will divide again (green check). Additionally, cells wherein the copy number of any chromosome falls to zero or surpasses 6 are removed (red x). After this, the cycle repeats. See Materials and methods for further details.

Figure 1—figure supplement 1
Download asset Open asset
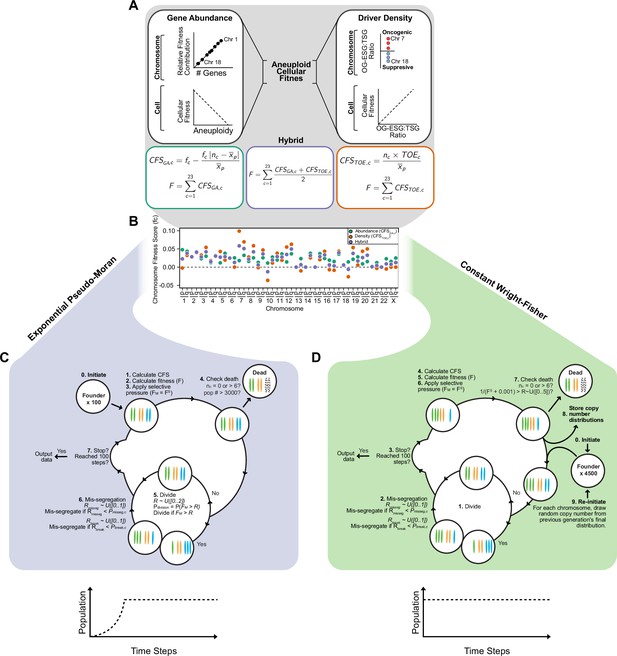
Expanded model of chromosome mis-segregation and karyotypic selection.

Models of selection on aneuploid karyotypes. Left. In the Gene Abundance model, chromosomes that encode a larger number of genes contribute more to cellular fitness (F). Thus, large chromosomes have a higher fitness score (fc). Deviation from the average ploidy of the population results in a reduced Contextual Fitness Score (CFS) for each chromosome, the sum of which represents the fitness of the cell. Right. In the Driver Density Model, the fitness contribution of a chromosome depends on the ratio of oncogenes and essential genes to tumor suppressors (OG-ESG:TSG). Gaining chromosomes with a higher OG-ESG:TSG ratio provides a fitness advantage while gaining more suppressive chromosomes invokes a fitness cost. These scores are still normalized to the ploidy of the average ploidy of the population to ensure that higher ploidy populations are not arbitrarily more fit. Middle. The Hybrid model takes the average of the fitness scores calculated in the other models. The neutral selection model (not shown) treats all karyotypes as equally fit. Base chromosome arm fitness scores for each model. Only the Hybrid and Driver Density model have negatively scored chromosomes, meaning their loss provides a fitness benefit. The neutral selection model does not require chromosome arm fitness scores. Simulating CIN in exponentially growing populations with pseudo-Moran limits. (0) Populations are founded by 100 founder cells and the simulation is initiated. (1) CFS values are calculated for each chromosome in a cell according to the chosen model. (2) Cellular fitness is calculated based on CFS values. (3) Selective pressure (S) is applied on cellular fitness values (F). (4) Cells are checked to see if any death conditions are met and if the population limit is met. (5) Cells probabilistically enter mitosis if their fitness value exceeds a random float (R) between 0 and 2. Thus Pdivision = P(FM >R). If a cell does not divide, it skips the next step. (6) If a cell enters mitosis, each chromosome has an opportunity to mis-segregate probabilistically. For each chromosome, a mis-segregation occurs if a random float (R), from 0 to 1, falls below Pmisseg. After a chromosome mis-segregation is determined, the chromosome arms may be individually segregated (i.e. reciprocal CNA) if a random float (R), from 0 to 1, falls below Pbreak. The cycle repeats and new CFS values are calculated, unless (7) stop conditions are met. When populations reach or exceed 3500 cells, a random half of the population is eliminated and the remaining cells continue the cycle. Simulating CIN in constant-size populations with Wright-Fisher dynamics. (0) Populations are initiated by 4500 euploid cells which (1) divide every step. (2) Chromosomes are mis-segregated as in the exponential pseudo-Moran model described above. (3) If stop conditions are met, the simulation ends and data are exported. If the cycle continues, (4) CFS values are calculated and used to (5) determine cellular fitness, after which, (6) selective pressure is applied. (7) Cells die if they lose both copies of a chromosome or exceed the upper limit of six. Additionally, to approximate Wright-Fisher dynamics, cells die if 1/(FS +0.001) exceeds a random float from 0 to 5. Thus, the baseline rate of cell death is ~0.2. (8) Each chromosome copy number is stored and the population is re-initiated with 4500 new cells. The copy numbers for each of new cell’s chromosomes are randomly and independently drawn from the copy number distributions of the previous generation. The cycle then repeats until the simulation ends (step 3).

Figure 1—figure supplement 2
Download asset Open asset
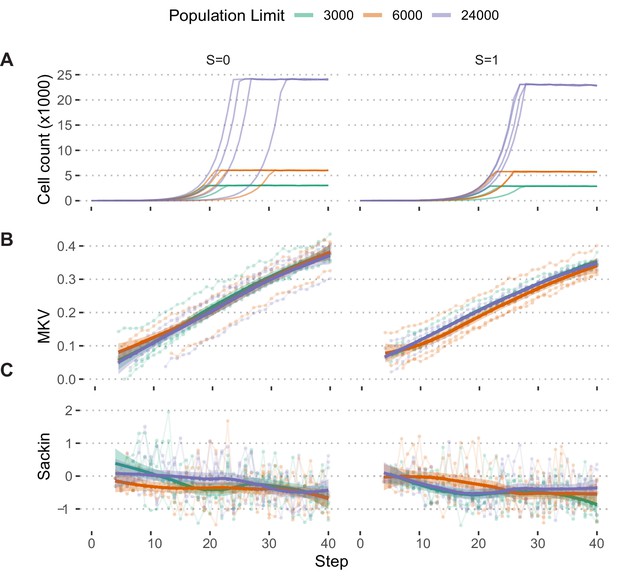
Population growth limits do not bias population measures.

(A) Growth curves of populations simulated under the Hybrid selection model and exponential pseudo-Moran growth model with S ∈[0,1] and Pmisseg misseg = 0.022 and limited to 3000, 6000, and 24,000 cells (n = 4 simulations each). (B) MKV (normalized to mean ploidy of the population) values steadily increase over time. (C) Loess regression curves show no significant deviations based on the population threshold, regardless of selection. Tree-tip-normalized Sackin index values for each population over time. No significant deviations based on the population threshold, regardless of selection.

Figure 2 with 2 supplements
Download asset Open asset
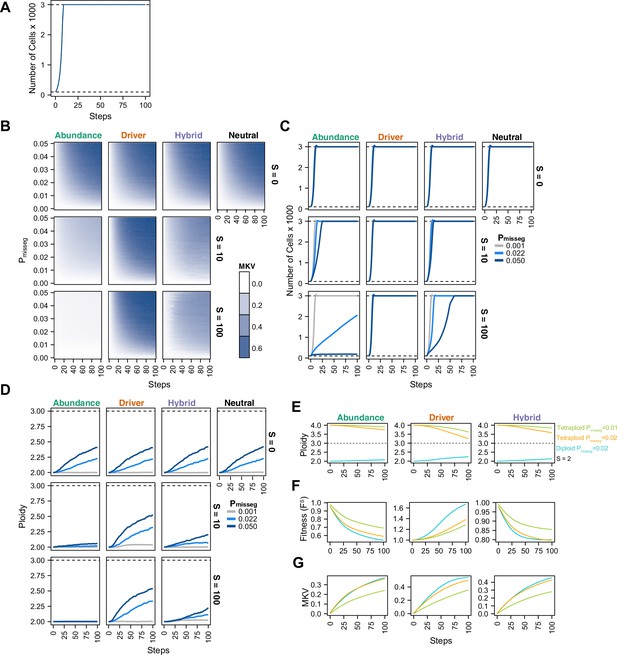
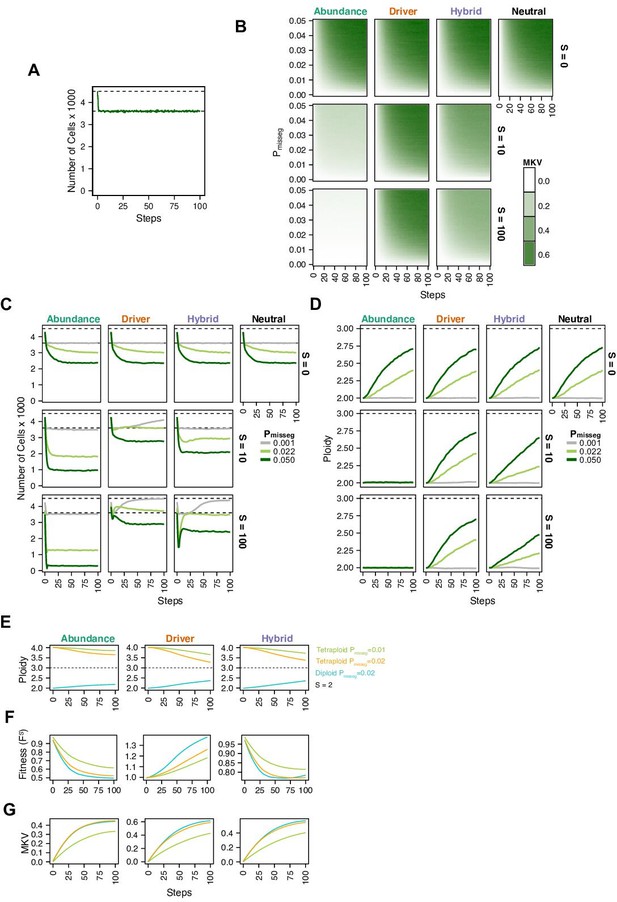
Evolutionary dynamics imparted by CIN.

(A) Population growth curve in the absence of selective pressure (Pmisseg = 0.001, S = 0, n = 3 simulations). The steady state population in null selection conditions is 3000 cells. (B) Heatmaps depicting dynamics of karyotype diversity as a function of time (steps), mis-segregation rate (Pmisseg), and selection (S) under each model of selection. Columns represent the same model; rows represent the same selection level. Mean karyotype diversity (MKV) is measured as the variance of each chromosome averaged across all chromosomes 1–22, and chromosome X. Low and high MKV are shown in white and blue respectively (n = 3 simulations for every combination of parameters). (C) Population growth under each model, varying Pmisseg and S. Pmisseg∈ [0.001, 0.022, 0.050] translate to about 0.046, 1, and 2.3 mis-segregations per division respectively for diploid cells. (D) Dynamics of the average ploidy (total # chromosome arms / 46) of a population while varying Pmisseg and S. (E) Dynamics of ploidy under each model for diploid and tetraploid founding populations. Pmisseg∈ [0.01, 0.02] translate to about 0.46 and 0.92 mis-segregations for diploid cells and 0.92 and 1.84 mis-segregations for tetraploid cells. (F) Fitness (FS) over time for diploid and tetraploid founding populations evolved under each model. (G) Karyotype diversity dynamics for diploid and tetraploid founding populations. MKV is normalized to the mean ploidy of the population at each time step. Plotted lines in C-G are local regressions of n = 3 simulations.

Figure 2—figure supplement 1
Download asset Open asset
Chromosomal instability and karyotype selection in constant-size populations approximating Wright-Fisher dynamics.

(A) Population size over time in the absence of selective pressure (Pmisseg = 0.001, S = 0, n = 3 simulations). The steady state population in null selection conditions is ~3600 cells as data is exported before populations are re-initiated. Dashed line represents the population at (re-)initiation (4500 cells). (B) Heatmaps depicting dynamics of karyotype diversity as a function of time (steps), mis-segregation rate (Pmisseg), and selection (S) under each model of selection. Columns represent the same model; rows represent the same selection level. Mean karyotype diversity (MKV) is measured as the variance of each chromosome averaged across all chromosomes 1–22, and chromosome X. Low and high MKV are shown in white and green respectively (n = 3 simulations for every combination of parameters). (C) Population growth under each model, varying Pmisseg and S. Pmisseg∈ [0.001, 0.022, 0.050] translate to about 0.046, 1, and 2.3 mis-segregations per division respectively for diploid cells. Top dashed line represents the population at (re-)initiation (4500 cells). Bottom dashed line represents the steady state population in selection-null conditions. (D) Dynamics of the average ploidy (total # chromosome arms / 46) of a population while varying Pmisseg and S. (E) Dynamics of ploidy under each model for diploid and tetraploid founding populations. Pmisseg∈ [0.01, 0.02] translate to about 0.46 and 0.92 mis-segregations for diploid cells and 0.92 and 1.84 mis-segregations for tetraploid cells. (F) Fitness (FS) over time for diploid and tetraploid founding populations evolved under each model. (G) Karyotype diversity dynamics for diploid and tetraploid founding populations. MKV is normalized to the mean ploidy of the population at each time step. Plotted lines in C-G are local regressions of n = 3 simulations.

Figure 2—figure supplement 2
Download asset Open asset
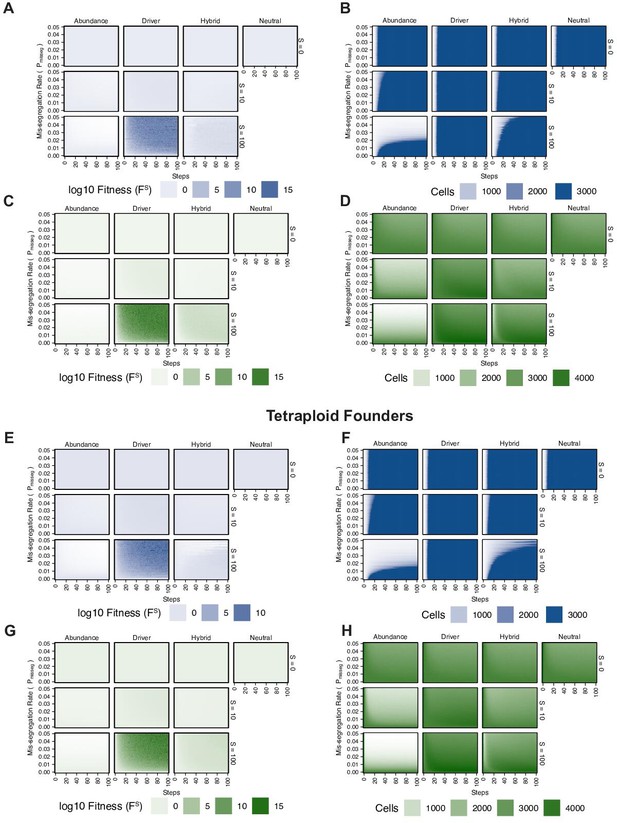
Fitness of diploid and tetraploid CIN +populations.

(A) Fitness landscape of simulations founded by diploid cells under exponential pseudo-Moran growth dynamics. (B) Size of simulated populations founded by diploid cells under exponential pseudo-Moran growth dynamics. (C) Fitness landscape of simulations founded by diploid cells under constant Wright-Fisher growth dynamics. (D) Size of simulated populations founded by diploid cells under constant Wright-Fisher growth dynamics. (E) Fitness landscape of simulations founded by tetraploid cells under exponential pseudo-Moran growth dynamics. (F) Size of simulated populations founded by tetraploid cells under exponential pseudo-Moran growth dynamics. (G) Fitness landscape of simulations founded by tetraploid cells under constant Wright-Fisher growth dynamics. (H) Size of simulated populations founded by tetraploid cells under constant Wright-Fisher growth dynamics.

Figure 3 with 1 supplement
Download asset Open asset
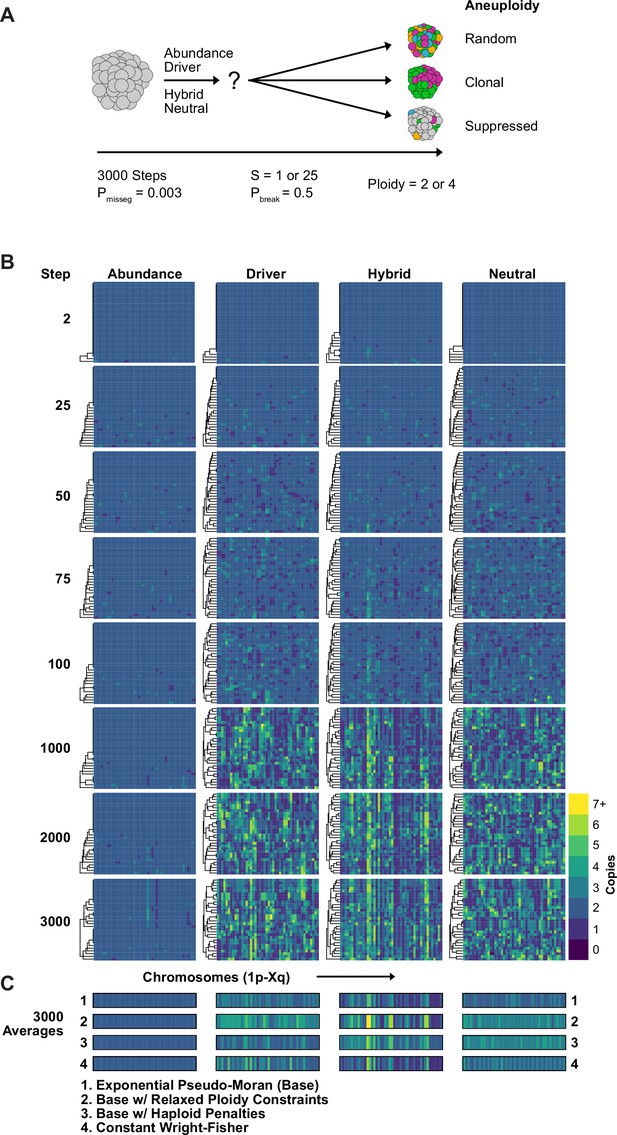
Karyotype diversity depends profoundly on selection modality.

(A) Simulation scheme to assess long-term dynamics of karyotype evolution and karyotype convergence. (B) Heatmaps depicting the chromosome copy number profiles of a subset (n = 30 out of 300 sampled cells) of the simulated population with early CIN over time under each model of karyotype selection. (C) Average heatmaps (lower) show the average copy number across the 5 replicates for (1) the Exponential Psuedo-Moran (Base), (2) the base model with the upper copy number limit set to 10, (3) the base model that invokes a FM x 0.1 penalty for any cell with a haploid chromosome, (4) and the Constant Population-Size Wright-Fisher model. Pmisseg = 0.003; S = 25 (except Neutral model; S = 0); ploidy = 2.

Figure 3—figure supplement 1
Download asset Open asset
Modeled population measures tracked over time.

(A) Average population ploidy over time for each selection model within each model variation. Data represent the mean and range (vertical lines) across five replicates for every 50 time steps in diploid populations with low selective pressure (light red) and high selective pressure (dark red) and tetraploid populations with low selective pressure (light blue) and high selective pressure (dark blue). (B) Average population fitness (log10) over time for each selection model within each model variation. Data represent the mean and range (vertical lines) across five replicates for every 50 time steps in diploid populations with low selective pressure (light red) and high selective pressure (dark red) and tetraploid populations with low selective pressure (light blue) and high selective pressure (dark blue). (C) Mean karyotype variance over time for each selection model within each model variation. Data represent the mean and range (vertical lines) across five replicates for every 50 time steps in diploid populations with low selective pressure (light red) and high selective pressure (dark red) and tetraploid populations with low selective pressure (light blue) and high selective pressure (dark blue).

Figure 4
Download asset Open asset
Topological features of simulated phylogenies delineate CIN rate and karyotype selection.

(A) Quantifiable features of karyotypically diverse populations. Heterogeneity between and within karyotypes is described by MKV and aneuploidy (inter- and intra-karyotype variance, see Materials and methods). We also quantify discrete topological features of phylogenetic trees, such as cherries (tip pairs) and pitchforks (3-tip groups), and a whole-tree measure of imbalance (or asymmetry), the Colless index. (B) Scheme to test how CIN and selection influence the phylogenetic topology of simulated populations. (C) Computed heterogeneity (aneuploidy and MKV) and topology (Colless index, cherries, pitchforks) summary statistics under varying Pmisseg and S values. MKV is normalized to the average ploidy of the population. Topological measures are normalized to population size. Spearman rank correlation coefficients (r) and p-values are displayed (n = 8 simulations). (D) Representative phylogenies for each hi/low CIN, hi/low selection parameter combination and their computed summary statistics. Each phylogeny represents n = 50 out of 300 cells for each simulation. (E) Dimensionality reduction of all simulations for each hi/low CIN, hi/low selection parameter combination using measures of karyotype heterogeneity only (left; MKV and aneuploidy) or measures of karyotype heterogeneity and phylogenetic topology (right; MKV, aneuploidy, Colless index, cherries, and pitchforks).

Figure 5 with 5 supplements
Download asset Open asset
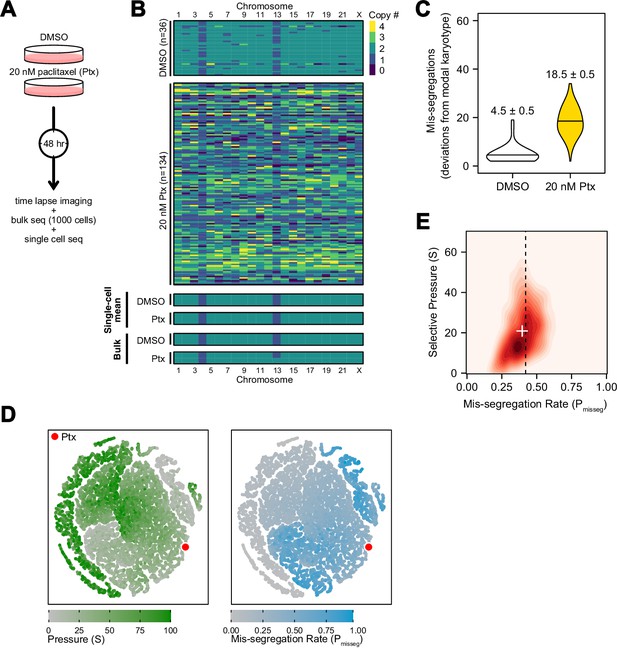
Experimental chromosome mis-segregation measured by Bayesian inference experimental scheme.

(A) Cal51 cells were treated with either DMSO or 20 nM paclitaxel for 48 hr prior to further analysis by time lapse imaging, bulk DNA sequencing, and scDNAseq. (B) Heatmaps showing copy number profiles derived from scDNAseq data, single-cell copy number averages, and bulk DNA sequencing. (C) Observed mis-segregations calculated as the absolute sum of deviations from the observed modal karyotype of the control. (D) Dimensionality reduction analysis of population summary statistics (aneuploidy, MKV, Colless index, cherries) from the first three time steps of all simulations performed under the Hybrid model. (E) 2D density plot showing joint posterior distributions from ABC analysis using population summary statistics computed from the paclitaxel-treated cells using the following priors and parameters: Growth Model = ‘exponential pseudo-Moran’, Selection Model = ‘Hybrid, initial ploidy = 2, 2 time steps, S ∈[0, 2… 100], Pmisseg∈[0, 0.005… 1.00] and a tolerance threshold of 0.05 to reject dissimilar simulation results. (see Materials and Methods). Vertical dashed line represents the experimentally observed mis-segregation rate. White + represents the mean of inferred values.

Figure 5—figure supplement 1
Download asset Open asset
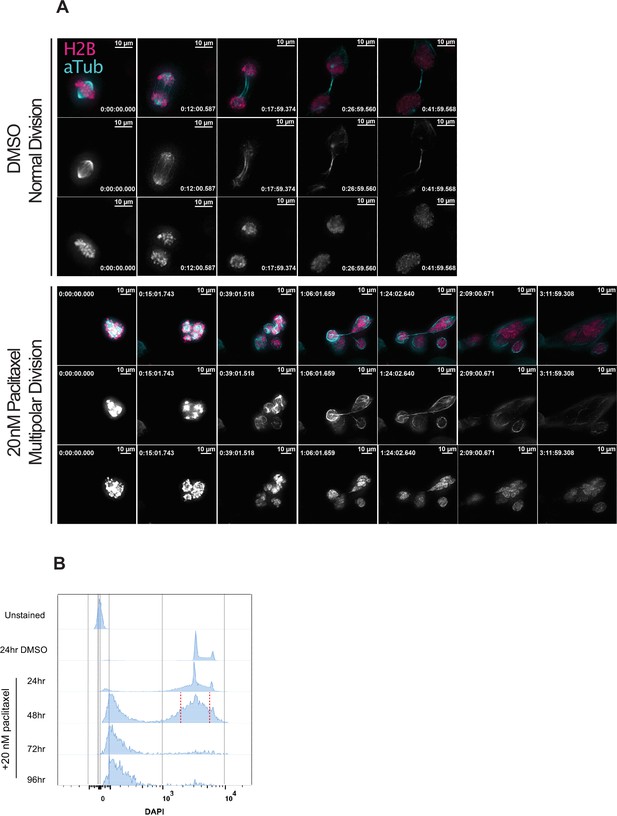
Induction of extensive chromosome mis-segregation via paclitaxel.

(A) Immunofluorescence time lapse montage of control Cal51 cells undergoing normal mitosis (top) and paclitaxel-treated treated cells undergoing a multipolar anaphase (middle) and partial cytokinesis failure (bottom). (B) Cell cycle profiles from flow cytometric analysis of Cal51 cells treated with either DMSO (72 hr) or 20 nM paclitaxel for 24, 48, or 72 hr. For FACS, cells treated for 48 hr were sorted into individual wells of 96-well plates. Sorting gate is shown by the red, dashed line.

Figure 5—figure supplement 2
Download asset Open asset
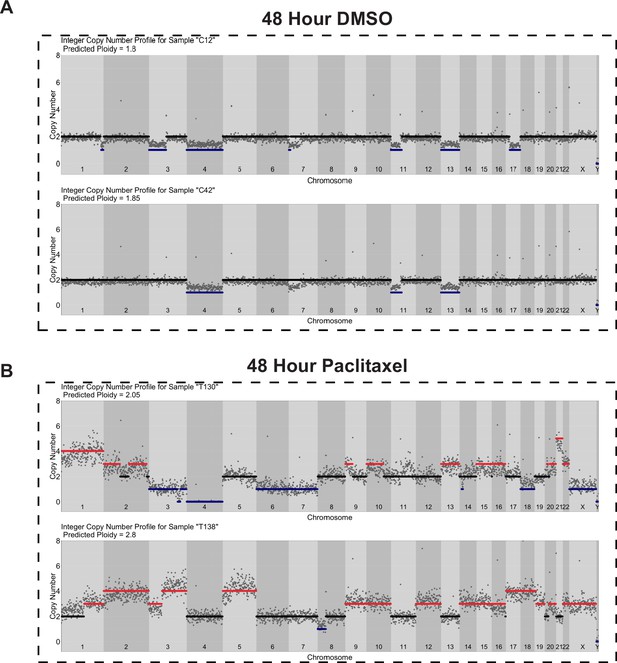
Copy number profiles of DMSO- and paclitaxel-treated Cal51 cells.

Single-cell copy number profiles for single (A) DMSO- and (B) paclitaxel-treated cells. A total of 500 Kb genomic bins and DNA content from FACS were used for copy number calculations (see Materials and methods).

Figure 5—figure supplement 3
Download asset Open asset
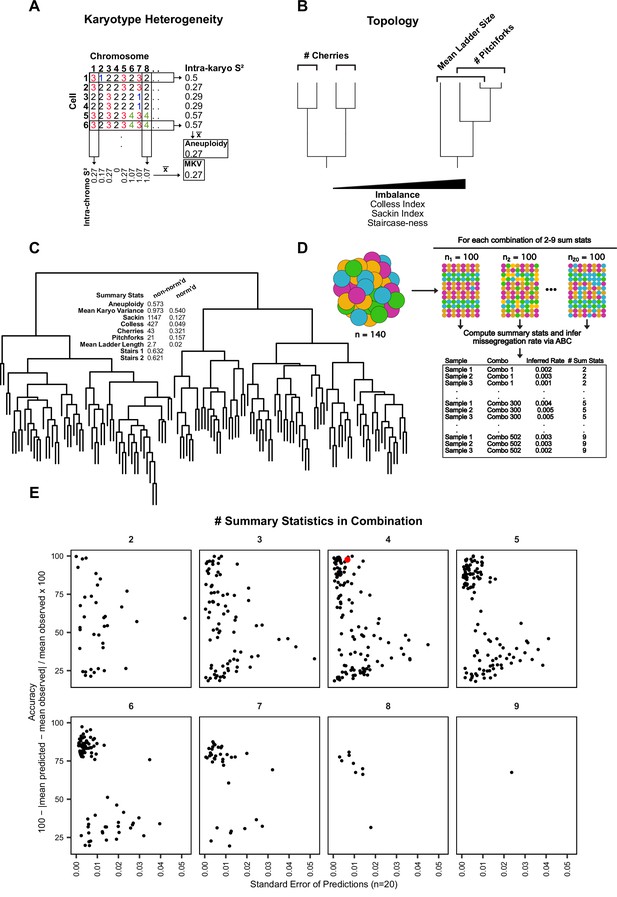
Summary statistic optimization for ABC.

(A) Schematic showing calculation of aneuploidy and MKV. (B) Examples of phylogenetic topology metrics. (C) Phylogenetic reconstruction of a population of Cal51 cells treated with 20 nM paclitaxel for 48 hr and associated heterogeneity and topology metrics. Normalized and non-normalized summary statistics are displayed (see Materials and methods). (D) Analytical scheme to identify most accurate and least variable combinations of heterogeneity and topology metrics. For each combination of 2–9 metrics, we iteratively re-sampled and remeasured the rate of mis-segregation in 100 random cells, three times, from our original dataset of paclitaxel-treated Cal51 cells. The red data point denotes our chosen combination for future analyses—average aneuploidy, MKV, Colless Index, and Cherries. This combination both limits redundant measures (i.e. Colless and Sackin indices) and contains both heterogeneity and topology metrics. (E) Percent accuracy and standard error of the mean for three sampled measurements of 100 paclitaxel-treated cells from the original population, repeated for each combination of heterogeneity and topology measures.

Figure 5—figure supplement 4
Download asset Open asset
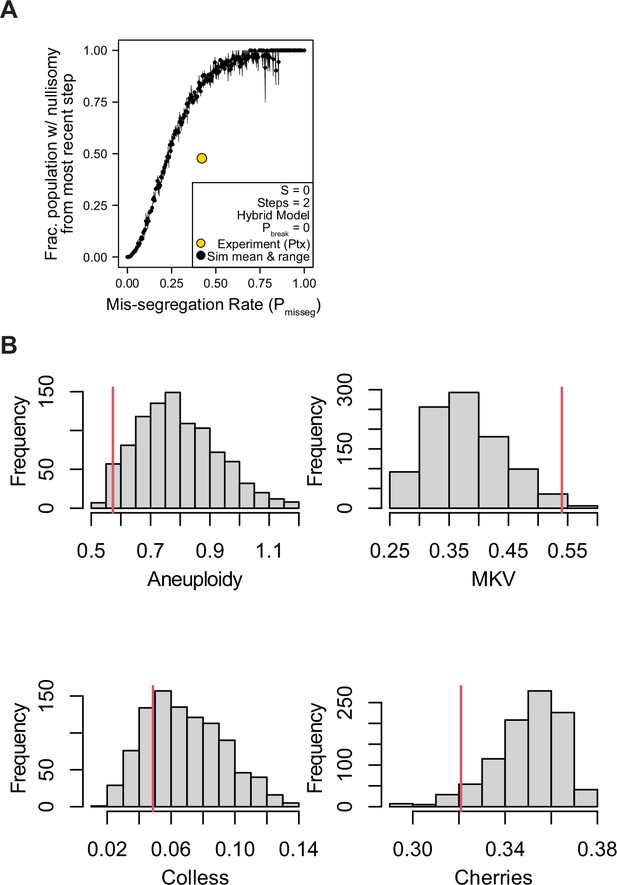
Nullisomy and posterior predictive checks of summary statistics from paclitaxel-treated Cal51 cells.

(A) Observed incidence of nullisomy in paclitaxel-treated cells plotted against the observed mis-segregation rate (Pmisseg,true = 18.5/44 = 0.42) overlaid on simulated data from the second time step (2 generations) under the Hybrid model with S = 0 and Pbreak = 0 (n = 3 simulations). (B) Posterior distributions of summary statistics from accepted simulations most similar to the paclitaxel-treated Cal51 cells (threshold = 0.05). The red line indicates the observed statistic in paclitaxel-treated cells. Colless index and cherry count is normalized to population size. MKV is normalized to the average ploidy of the population.

Figure 5—figure supplement 5
Download asset Open asset
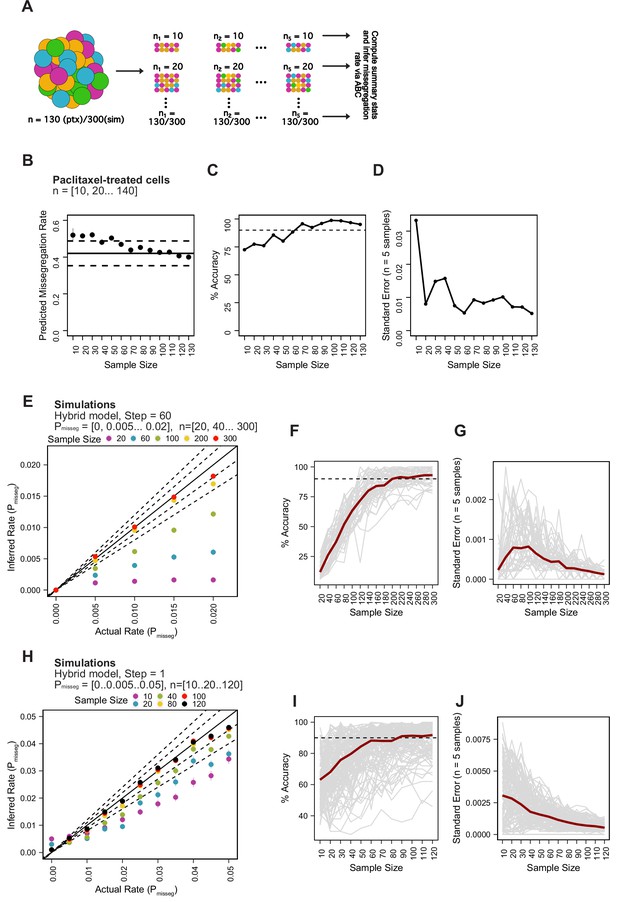
Minimum sampling of karyotype heterogeneity.

(A) Analytical scheme to optimize the number of cells to sample for measuring mis-segregation rates from karyotype heterogeneity. We iteratively re-sampled and remeasured the rate of mis-segregation for a range of sample sizes (n = 5 random samples). (B) Predicted mis-segregation rates over a range of sample sizes (n = 5 samples). Points and error bars are the mean ± standard error. Black solid line denotes the mean observed rate of mis-segregation induced by 20 nM paclitaxel. Black dashed lines are half the standard deviation of observed mis-segregation rates per cell. (C) Mean percent accuracy of ABC-inferred rates of mis-segregation due to paclitaxel taken from each set of five random samples using the observed rate of mis-segregation as the ‘true value’. Calculated as Mean%accuracy=100−(true−meaninferredtrue×100). Dashed lines represent 90% accuracy. (D) Standard error of ABC-inferred rates of mis-segregation for each set of random samples from paclitaxel-treated cells. (E) ABC-inferred mis-segregation rates by sample size from simulations with known parameters (n = 5 samples). Points represent mean ± standard error across 5 samples for each of 11 selective pressure (S) values. Solid line represents a perfect correlation. Inner dashed line represent ±10% margin. Outer dashed line represents ±20% margin. Simulation parameters: Pmisseg∈ [0, 0.005… 0.02], time steps = 60, Selection Model = ‘Hybrid’, Growth Model = ‘exponential pseudo-Moran’, S = [0, 10... 100], and a tolerance threshold of 0.05. (F) Mean percent accuracy of ABC-inferred rates of mis-segregation in simulations (parameters in E) taken at various sample sizes. Gray lines represent the mean percent accuracy of five random samples for each sample size for the same simulated population (n = 55 simulations). The dashed line represents 90% accuracy. Calculated as described above but taking the known simulation parameter as the ‘true’ value. (G) Standard error of ABC-inferred rates of mis-segregation in simulations (parameters in E) taken at various sample sizes. Gray lines represent the standard error of five random samples for each sample size for the same simulated population (n = 55 simulations). (H) ABC-inferred mis-segregation rates by sample size from simulations with known parameters (n = 5 samples). Points represent mean ± standard error across 5 samples for each of 11 selective pressure (S) values. Solid line represents a perfect correlation. Inner dashed line represent ±10% margin. Outer dashed line represents ±20% margin. ABC was performed with the following parameters and priors: Pmisseg∈[0, 0.005… 0.05], time steps = 1, Selection Model = ‘Hybrid’, Growth Model = ‘exponential pseudo-Moran’, S ∈ [0, 10… 100], and a tolerance threshold of 0.05. (I) Mean percent accuracy of ABC-inferred rates of mis-segregation in simulations (parameters in H) taken at various sample sizes. Gray lines represent the mean percent accuracy of five random samples for each sample size for the same simulated population (n = 121 simulations). The dashed line represents 90% accuracy. (J) Standard error of ABC-inferred rates of mis-segregation in simulations (parameters in H) taken at various sample sizes. Gray lines represent the standard error of five random samples for each sample size for the same simulated population (n = 121 simulations). Note: Red lines in F, G, I, and J represent the median.

Figure 6 with 5 supplements
Download asset Open asset
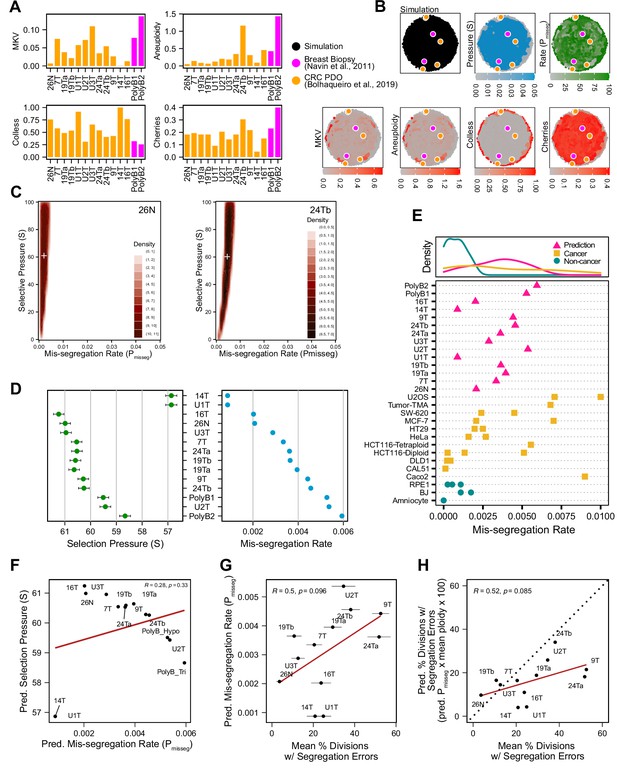
Inferring chromosome mis-segregation rates in tumors and organoids Bolhaqueiro et al., 2019Navin et al., 2011.

(A) Computed population summary statistics for colorectal cancer (CRC) patient-derived organoids (PDOs) and breast biopsy scDNAseq datasets from Bolhaqueiro et al., 2019 (gold) and Navin et al., 2011 (pink). (B) Dimensionality reduction analysis of population summary statistics showing biological observations overlaid on, and found within, the space of simulated observations. Point colors show the simulation parameters and summary statistics for all simulations using the following priors and parameters: Growth Model = ‘exponential pseudo-Moran’, Selection Model = ‘Abundance’, initial ploidy = 2, time steps ∈[40, 41… 80], S ∈[0,2… 100], Pmisseg∈[0,0.001… 0.050] and a tolerance threshold of 0.05 to reject dissimilar simulation results. (see Materials and Methods). (C) 2D density plots showing joint posterior distributions of Pmisseg and S values from the approximate Bayesian computation analysis of samples 26 N (left) and 24Tb (right) from Bolhaqueiro et al., 2019. White + represents the mean of inferred values. (D) Inferred selective pressures and mis-segregation rates from each scDNAseq dataset (mean and SEM of accepted values). (E) Predicted mis-segregation rates in CRC PDOs and a breast biopsy plotted with approximated mis-segregation rates observed in cancer (blue triangle) and non-cancer (red circle) models (primarily cell lines) from previous studies (Table 5; see Materials and methods). The predicted mis-segregation rates in these cancer-derived samples fall within those observed in cancer cell lines and above those of non-cancer cell lines. (F) Pearson correlation of predicted mis-segregation rates and predicted selective pressures in CRC PDOs from Bolhaqueiro et al., 2019. (G) Pearson correlation of predicted mis-segregation rates and the incidence of observed segregation errors in CRC PDOs from Bolhaqueiro et al., 2019. Error bars represent SEM values. (H) Pearson correlation of observed incidence of segregation errors in CRC PDOs from Bolhaqueiro et al., 2019 to the ploidy-corrected prediction of the observed incidence of segregation errors. These values assume the involvement of 1 chromosome per observed error and are calculated as the (predicted mis-segregation rate) x (mean number of chromosomes observed per cell) x 100. Dotted line = 1:1 reference.

Figure 6—figure supplement 1
Download asset Open asset
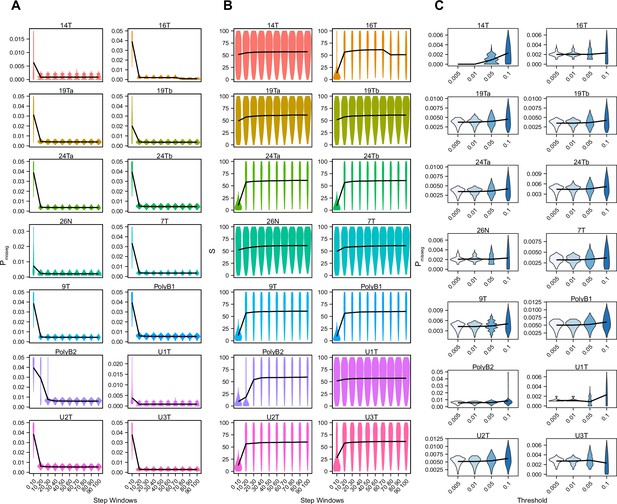
ABC-inference threshold and step-window analysis.

Posterior distributions of mis-segregation rates (A) and selective pressure, S (B) inferred using ABC analysis of CRC organoids and a breast biopsy from Bolhaqueiro et al., 2019 and Navin et al., 2011 respectively using a sliding window prior distribution of time steps. ABC was performed for every interval of 10 steps between 0 and 100 using a tolerance threshold of 0.05. Schematic of analysis shown below. ABC was performed with the following parameters and priors: Pmisseg∈ [0...0.001...0.05], S ∈ [0...2...100], indicated time step window, Selection Model = ‘Abundance’, Growth Model = ‘exponential pseudo-Moran’, and a tolerance threshold of 0.05. (C) Posterior distributions of mis-segregation rates inferred using ABC analysis on the same samples as in A using tolerance thresholds of 0.005, 0.01, 0.05, 0.1. ABC was performed with the following parameters and priors: Pmisseg∈ [0, 0.001… 0.05], S ∈ [0, 2… 100], time steps ∈ [40, 41… 80], Selection Model = ‘Abundance’, Growth Model = ‘exponential pseudo-Moran’, and the indicated tolerance threshold.

Figure 6—figure supplement 2
Download asset Open asset
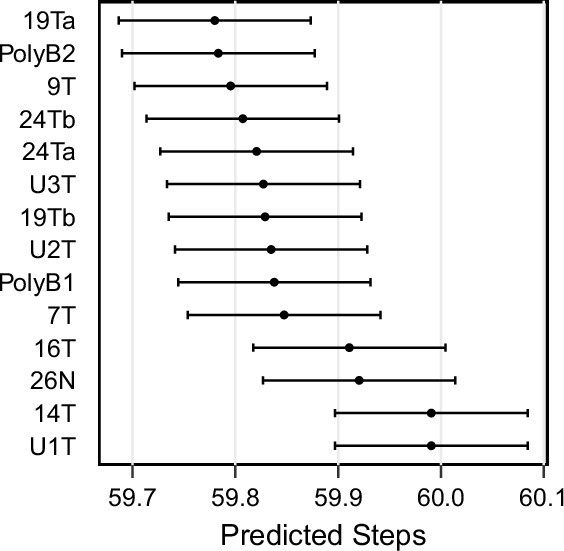
ABC-inferred step count in patient-derived samples.

Mean and standard error for steps in each patient-derived sample (accompanying data in Figure 6), inferred via approximate Bayesian computation.

Figure 6—figure supplement 3
Download asset Open asset
ABC-inferred mis-segregation rates and selective pressures in patient-derived samples.

Joint (2D density plots) and individual (1D density plots) distributions of mis-segregation rates and selective pressures in patient-derived CRC organoids and a breast biopsy from Bolhaqueiro et al., 2019 and Navin et al., 2011 respectively (accompanying data in Figure 6). The prior (yellow) distribution represents the parameters used for simulation while the posterior (gray) distribution represents the parameters from simulations whose observed measurements were similar to the measurements taken from the patient-derived sample using a tolerance threshold of 0.05. White + signs on joint distributions represent the mean of both parameters.

Figure 6—figure supplement 4
Download asset Open asset
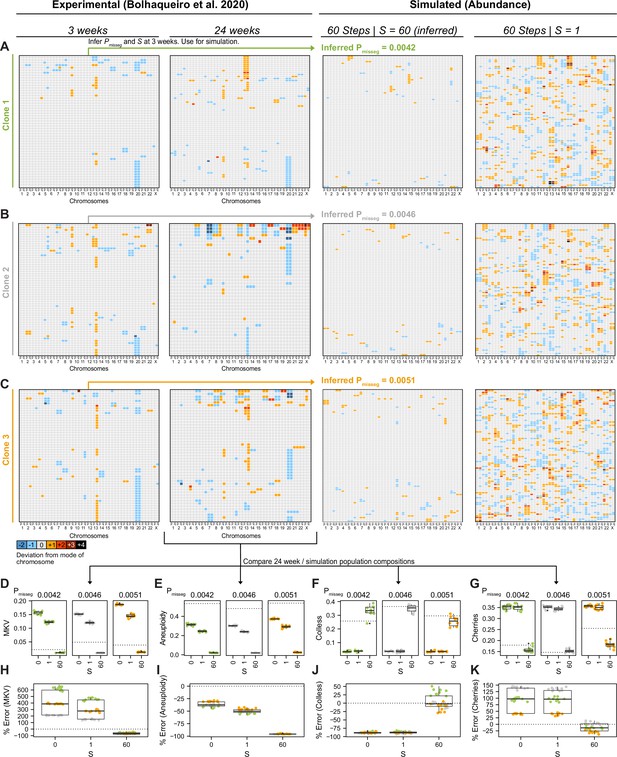
Validation of selection in longitudinally sequenced CRC organoids.

(A–C) Copy number heatmaps showing the deviation from the mode of each chromosome derived from longitudinally sequenced clonal organoids from Bolhaqueiro et al., 2019. ABC was performed on scDNAseq data from three clones at 3 weeks of growth. The resulting inferred mis-segregation rate (Pmisseg) and selective pressure (S) were used to simulate CIN and selection in these clones over 60 time steps, at which point the composition of the populations were compared to the scDNAseq data from each of the clones at 24 weeks of growth (D–K). Additional simulations using S = 0 (not shown) and S = 1 were also performed. Inferred Pmisseg values for (A) clone 1, (B) clone 2, and (C) clone 3 were 0.0042, 0.0046, and 0.0051 respectively. S = 60 was inferred for each clone. ABC was performed on the 3 week data with the following parameters and priors: Pmisseg∈ [0, 0.001... 0.05], S ∈ [0, 2… 100], time steps ∈ [40, 41... 80], Selection Model = ‘Abundance’, Growth Model = ‘exponential pseudo-Moran’, and a tolerance threshold of 0.05. (D) MKV values from n = 10 simulations per clone. Dotted line represents the MKV value observed in the scDNAseq data. (E) Aneuploidy values from n = 10 simulations per clone per S value. Dotted line represents the Aneuploidy value observed in the scDNAseq data. (F) Colless index values from n = 10 simulations per clone S value. Dotted line represents the Colless index value observed in the scDNAseq data. (G) Normalized cherry values from n = 10 simulations per clone S value. Dotted line represents the normalized cherry value observed in the scDNAseq data. (H) Percent error for MKV observations in n = 10 simulations per clone per S value. Dotted line represents 0% error. (I) Percent error for aneuploidy observations in n = 10 simulations per clone per S value. Dotted line represents 0% error. (J) Percent error for Colless observations in n = 10 simulations per clone per S value. Dotted line represents 0% error. (K) Percent error for normalized cherry observations in n = 10 simulations per clone per S value. Dotted line represents 0% error.

Figure 6—figure supplement 5
Download asset Open asset
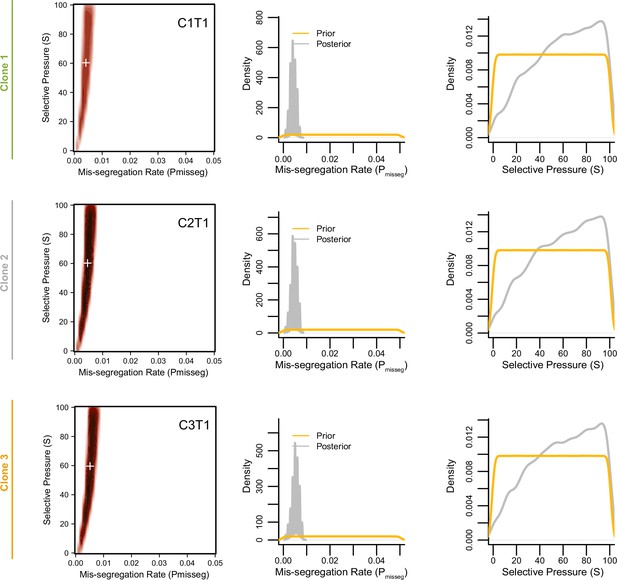
Joint posterior distributions from CRC organoids at 3 weeks.

Joint (2D density plots) and individual (1D density plots) distributions of mis-segregation rates and selective pressures in individual clones of a patient-derived CRC organoid line from Bolhaqueiro et al., 2019 after 3 weeks of growth (accompanying data in Figure 6—figure supplement 4). The prior (yellow) distribution represents the parameters used for simulation while the posterior (gray) distribution represents the parameters from simulations whose observed measurements were similar to the measurements taken from the patient-derived sample using a tolerance threshold of 0.05. White + signs on joint distributions represent the mean of both parameters.

Tables

Table 1
Base chromosome-specific fitness scores for individual models.
Selection model
CHR ARMGene AbundanceDriver DensityHybrid
1p0.04780162–0.00240180.02269992
1q0.043403210.032443620.03792341
2p0.027336550.029357170.02834686
2q0.042440540.039432670.0409366
3p0.023104120.032896950.02800053
3q0.02997560.054167360.04207148
4p0.012381950.017849090.01511552
4q0.031817960.029013240.0304156
5p0.011784430.042811660.02729805
5q0.037876150.019499340.02868775
6p0.025577190.023986190.02478169
6q0.025543990.000116250.01283012
7p0.01795880.098892840.05842582
7q0.032315890.069333140.05082451
8p0.015917280.027695640.02180646
8q0.02549420.058614270.04205423
9p0.01301266–0.00129410.00585929
9q0.025726570.047026810.03637669
10 p0.0112201–0.0364218–0.0126008
10q0.027502530.011426880.01946471
11 p0.019618580.038186210.0289024
11q0.036299360.018987840.0276436
12 p0.01425750.05515510.0347063
12q0.036598120.062737860.04966799
13 p000
13q0.02333649–0.01015390.00659128
14 p1.66E-0508.30E-06
14q0.037925940.025574390.03175016
15 p000
15q0.037013060.02065660.02883483
16 p0.023834420.043347360.03359089
16q0.01900446–0.00714440.00593005
17 p0.01548573–0.00859750.00344414
17q0.035535860.043634740.0395853
18 p0.006273960.005336970.00580547
18q0.01434049–0.0263632–0.0060113
19 p0.021593720.053714160.03765394
19q0.028133250.005503380.01681831
20 p0.00896280.043510250.02623653
20q0.015269960.049935930.03260295
21 p0.0023236900.00116185
21q0.01233215–0.00330920.00451147
22 p0.0001327806.64E-05
22q0.02297134–0.00515810.0089066
Xp0.0155521300.00777606
Xp0.0249962700.01249813
Table 2
Parameters varied during agent-based modeling.
ParameterDescription
PmissegProbability of mis-segregation per chromosome per division
PbreakProbability of chromosome breakage after mis-segregation
PdivisionProbability of cellular division per time step
SMagnitude of selective pressure on aneuploid karyotypes
Table 3
Model selection.
SampleGrowt ModelSelectio ModelPPBF (Ho Neutral)PmissegSSteps
7Texponential pseudo-MoranAbundance0.621Inf0.0033 ± 1e-0560.5416 ± 0.205359.8475 ± 0.0937
7Texponential pseudo-MoranDriver0.14Inf0.001 ± 1e-0549.6557 ± 0.238958.7002 ± 0.0943
7Texponential pseudo-MoranHybrid0.239Inf8e-04 ± 1e-0549.3428 ± 0.237758.5789 ± 0.0935
7Texponential pseudo-MoranNeutral0NA9e-04 ± 5e-050 ± 057.7994 ± 0.6728
7Tconstant Wright-FisherAbundance0.985Inf0.0062 ± 2e-0569.7026 ± 0.172459.9318 ± 0.0937
7Tconstant Wright-FisherDriver0NA0.0012 ± 1e-0548.2881 ± 0.238457.5239 ± 0.0933
7Tconstant Wright-FisherHybrid0.015Inf9e-04 ± 1e-0550.7803 ± 0.235958.2514 ± 0.0941
7Tconstant Wright-FisherNeutral0NA9e-04 ± 5e-050 ± 058.7803 ± 0.6701
U1Texponential pseudo-MoranAbundance0.5821999e-04 ± 1e-0556.8672 ± 0.216859.9906 ± 0.0937
U1Texponential pseudo-MoranDriver0.113390.001 ± 1e-0549.6611 ± 0.238958.6886 ± 0.0944
U1Texponential pseudo-MoranHybrid0.156548e-04 ± 1e-0549.3658 ± 0.237558.569 ± 0.0935
U1Texponential pseudo-MoranNeutral0.14919e-04 ± 5e-050 ± 057.7102 ± 0.67
U1Tconstant Wright-FisherAbundance0.6542900.001 ± 1e-0561.4358 ± 0.202960.0021 ± 0.0937
U1Tconstant Wright-FisherDriver0.115510.0012 ± 1e-0548.2767 ± 0.238357.5267 ± 0.0934
U1Tconstant Wright-FisherHybrid0.115519e-04 ± 1e-0550.8033 ± 0.235858.2507 ± 0.0941
U1Tconstant Wright-FisherNeutral0.11519e-04 ± 5e-050 ± 058.7803 ± 0.6701
U2Texponential pseudo-MoranAbundance0.6282510.0054 ± 1e-0559.4269 ± 0.210859.8349 ± 0.0935
U2Texponential pseudo-MoranDriver0.079320.0027 ± 2e-0550.1513 ± 0.239657.4538 ± 0.0934
U2Texponential pseudo-MoranHybrid0.166660.0022 ± 2e-0548.7779 ± 0.241357.7078 ± 0.0934
U2Texponential pseudo-MoranNeutral0.12710.0021 ± 7e-050 ± 056.8535 ± 0.6619
U2Tconstant Wright-FisherAbundance0.91828170.0112 ± 3e-0569.7222 ± 0.170360.0655 ± 0.0934
U2Tconstant Wright-FisherDriver0.00140.0027 ± 2e-0548.7794 ± 0.238956.4812 ± 0.0919
U2Tconstant Wright-FisherHybrid0.0641960.0022 ± 1e-0550.9564 ± 0.237957.1161 ± 0.0925
U2Tconstant Wright-FisherNeutral0.01710.0022 ± 1e-040 ± 057.7898 ± 0.6841
U3Texponential pseudo-MoranAbundance0.5821990.0029 ± 1e-0560.9557 ± 0.209159.8273 ± 0.0938
U3Texponential pseudo-MoranDriver0.113390.001 ± 1e-0549.6707 ± 0.238958.6986 ± 0.0944
U3Texponential pseudo-MoranHybrid0.156548e-04 ± 1e-0549.3754 ± 0.237658.5711 ± 0.0935
U3Texponential pseudo-MoranNeutral0.14919e-04 ± 5e-050 ± 057.7102 ± 0.67
U3Tconstant Wright-FisherAbundance0.736Inf0.0052 ± 2e-0569.8357 ± 0.171359.932 ± 0.0934
U3Tconstant Wright-FisherDriver0.13Inf0.0012 ± 1e-0548.2864 ± 0.238357.5385 ± 0.0934
U3Tconstant Wright-FisherHybrid0.134Inf9e-04 ± 1e-0550.8219 ± 0.235758.2482 ± 0.0941
U3Tconstant Wright-FisherNeutral0NA9e-04 ± 5e-050 ± 058.8567 ± 0.6676
14Texponential pseudo-MoranAbundance0.5821999e-04 ± 1e-0556.8672 ± 0.216859.9906 ± 0.0937
14Texponential pseudo-MoranDriver0.113390.001 ± 1e-0549.6614 ± 0.23958.695 ± 0.0944
14Texponential pseudo-MoranHybrid0.156548e-04 ± 1e-0549.3716 ± 0.237558.5632 ± 0.0935
14Texponential pseudo-MoranNeutral0.14919e-04 ± 5e-050 ± 057.7102 ± 0.67
14Tconstant Wright-FisherAbundance0.6542900.0011 ± 1e-0562.8579 ± 0.207560.0029 ± 0.0936
14Tconstant Wright-FisherDriver0.115510.0012 ± 1e-0548.2967 ± 0.238357.5295 ± 0.0934
14Tconstant Wright-FisherHybrid0.115519e-04 ± 1e-0550.8274 ± 0.235758.2478 ± 0.0941
14Tconstant Wright-FisherNeutral0.11519e-04 ± 5e-050 ± 058.8567 ± 0.6676
16Texponential pseudo-MoranAbundance0.5821990.002 ± 1e-0561.2401 ± 0.202859.9109 ± 0.0935
16Texponential pseudo-MoranDriver0.113390.001 ± 1e-0549.6539 ± 0.238958.7006 ± 0.0943
16Texponential pseudo-MoranHybrid0.156548e-04 ± 1e-0549.3611 ± 0.237658.574 ± 0.0935
16Texponential pseudo-MoranNeutral0.14919e-04 ± 5e-050 ± 057.7994 ± 0.6728
16Tconstant Wright-FisherAbundance0.6542900.0038 ± 1e-0569.8456 ± 0.170159.9523 ± 0.0936
16Tconstant Wright-FisherDriver0.115510.0012 ± 1e-0548.261 ± 0.238457.5233 ± 0.0933
16Tconstant Wright-FisherHybrid0.115519e-04 ± 1e-0550.7713 ± 0.235958.2554 ± 0.0941
16Tconstant Wright-FisherNeutral0.11519e-04 ± 5e-050 ± 058.7803 ± 0.6701
19Taexponential pseudo-MoranAbundance0.7113130.004 ± 1e-0560.6391 ± 0.207459.7801 ± 0.0934
19Taexponential pseudo-MoranDriver0.038170.0028 ± 2e-0550.2185 ± 0.239957.3764 ± 0.0934
19Taexponential pseudo-MoranHybrid0.135590.0022 ± 3e-0548.3823 ± 0.24257.5368 ± 0.0935
19Taexponential pseudo-MoranNeutral0.11610.0022 ± 9e-050 ± 056.5955 ± 0.6549
19Taconstant Wright-FisherAbundance0.97117600.0075 ± 2e-0569.3863 ± 0.173559.956 ± 0.0938
19Taconstant Wright-FisherDriver000.0028 ± 2e-0548.8413 ± 0.239256.4529 ± 0.0917
19Taconstant Wright-FisherHybrid0.0263150.0023 ± 1e-0550.8588 ± 0.238357.1031 ± 0.0925
19Taconstant Wright-FisherNeutral0.00410.0023 ± 1e-040 ± 057.9522 ± 0.6869
19Tbexponential pseudo-MoranAbundance0.7273200.0036 ± 1e-0560.5885 ± 0.208559.829 ± 0.0938
19Tbexponential pseudo-MoranDriver0.03130.001 ± 1e-0549.6622 ± 0.238958.6929 ± 0.0944
19Tbexponential pseudo-MoranHybrid0.127568e-04 ± 1e-0548.5237 ± 0.232258.9663 ± 0.0931
19Tbexponential pseudo-MoranNeutral0.11619e-04 ± 5e-050 ± 057.7102 ± 0.67
19Tbconstant Wright-FisherAbundance0.979473200.0068 ± 2e-0569.5697 ± 0.17359.9232 ± 0.0935
19Tbconstant Wright-FisherDriver000.0012 ± 1e-0548.2786 ± 0.238357.5433 ± 0.0934
19Tbconstant Wright-FisherHybrid0.029829e-04 ± 1e-0550.8162 ± 0.235758.2495 ± 0.0941
19Tbconstant Wright-FisherNeutral0.00119e-04 ± 5e-050 ± 058.8376 ± 0.669
24Taexponential pseudo-MoranAbundance0.7313210.0036 ± 1e-0560.5303 ± 0.208259.8208 ± 0.0938
24Taexponential pseudo-MoranDriver0.029130.001 ± 1e-0549.6703 ± 0.238958.6938 ± 0.0944
24Taexponential pseudo-MoranHybrid0.125558e-04 ± 1e-0549.3669 ± 0.237658.5778 ± 0.0935
24Taexponential pseudo-MoranNeutral0.11619e-04 ± 5e-050 ± 057.7102 ± 0.67
24Taconstant Wright-FisherAbundance0.979473460.0068 ± 2e-0569.6173 ± 0.17359.933 ± 0.0934
24Taconstant Wright-FisherDriver000.0012 ± 1e-0548.2789 ± 0.238357.5377 ± 0.0934
24Taconstant Wright-FisherHybrid0.029569e-04 ± 1e-0550.8229 ± 0.235758.2524 ± 0.0941
24Taconstant Wright-FisherNeutral0.00119e-04 ± 5e-050 ± 058.8567 ± 0.6676
24Tbexponential pseudo-MoranAbundance0.682940.0046 ± 1e-0560.2602 ± 0.208459.8073 ± 0.0936
24Tbexponential pseudo-MoranDriver0.054230.0031 ± 3e-0550.2981 ± 0.239957.2927 ± 0.0934
24Tbexponential pseudo-MoranHybrid0.149650.0025 ± 4e-0548.3833 ± 0.24457.4236 ± 0.0936
24Tbexponential pseudo-MoranNeutral0.11810.0025 ± 0.000130 ± 056.7229 ± 0.6579
24Tbconstant Wright-FisherAbundance0.95477300.0215 ± 0.0001133.6703 ± 0.296259.9064 ± 0.0937
24Tbconstant Wright-FisherDriver020.003 ± 2e-0548.7528 ± 0.239356.4175 ± 0.0918
24Tbconstant Wright-FisherHybrid0.0393180.0024 ± 2e-0550.7006 ± 0.238957.107 ± 0.0925
24Tbconstant Wright-FisherNeutral0.00610.0024 ± 0.000110 ± 058.0318 ± 0.6822
26Nexponential pseudo-MoranAbundance0.5821990.0021 ± 1e-0560.9877 ± 0.203159.9205 ± 0.0934
26Nexponential pseudo-MoranDriver0.113390.001 ± 1e-0549.6389 ± 0.238958.7018 ± 0.0944
26Nexponential pseudo-MoranHybrid0.156548e-04 ± 1e-0549.3389 ± 0.237758.5755 ± 0.0935
26Nexponential pseudo-MoranNeutral0.14919e-04 ± 5e-050 ± 057.7994 ± 0.6728
26Nconstant Wright-FisherAbundance0.6542900.0039 ± 1e-0569.794 ± 0.170459.9547 ± 0.0935
26Nconstant Wright-FisherDriver0.115510.0012 ± 1e-0548.2849 ± 0.238457.5175 ± 0.0933
26Nconstant Wright-FisherHybrid0.115519e-04 ± 1e-0550.737 ± 0.235958.2609 ± 0.0941
26Nconstant Wright-FisherNeutral0.11519e-04 ± 5e-050 ± 058.7803 ± 0.6701
9Texponential pseudo-MoranAbundance0.6852990.0044 ± 1e-0560.2829 ± 0.208659.7955 ± 0.0936
9Texponential pseudo-MoranDriver0.052230.0029 ± 2e-0550.2323 ± 0.239857.3657 ± 0.0934
9Texponential pseudo-MoranHybrid0.147640.0022 ± 3e-0548.3829 ± 0.242257.5193 ± 0.0936
9Texponential pseudo-MoranNeutral0.11710.0023 ± 9e-050 ± 056.6083 ± 0.6581
9Tconstant Wright-FisherAbundance0.95892990.0087 ± 2e-0569.6836 ± 0.172459.926 ± 0.0937
9Tconstant Wright-FisherDriver010.0028 ± 2e-0548.8394 ± 0.239256.4465 ± 0.0917
9Tconstant Wright-FisherHybrid0.0373600.0023 ± 1e-0550.8477 ± 0.238457.0952 ± 0.0925
9Tconstant Wright-FisherNeutral0.00510.0023 ± 1e-040 ± 057.9427 ± 0.687
PolyB1exponential pseudo-MoranAbundance0.6352610.0053 ± 1e-0559.5088 ± 0.210459.8379 ± 0.0935
PolyB1exponential pseudo-MoranDriver0.076310.0028 ± 2e-0550.2364 ± 0.239857.4025 ± 0.0934
PolyB1exponential pseudo-MoranHybrid0.164670.0022 ± 3e-0548.6949 ± 0.241957.6322 ± 0.0934
PolyB1exponential pseudo-MoranNeutral0.12410.0022 ± 9e-050 ± 056.5955 ± 0.6549
PolyB1constant Wright-FisherAbundance0.92534820.0111 ± 3e-0570.2557 ± 0.16960.042 ± 0.0936
PolyB1constant Wright-FisherDriver0.00140.0028 ± 2e-0548.8194 ± 0.239156.4451 ± 0.0917
PolyB1constant Wright-FisherHybrid0.0612280.0023 ± 1e-0550.895 ± 0.238157.1073 ± 0.0925
PolyB1constant Wright-FisherNeutral0.01410.0023 ± 1e-040 ± 057.9809 ± 0.6861
PolyB2exponential pseudo-MoranAbundance0.6032180.0059 ± 1e-0558.6612 ± 0.21259.7835 ± 0.0937
PolyB2exponential pseudo-MoranDriver0.086310.0038 ± 4e-0550.2948 ± 0.239457.0217 ± 0.093
PolyB2exponential pseudo-MoranHybrid0.17610.004 ± 7e-0548.9466 ± 0.247257.28 ± 0.0942
PolyB2exponential pseudo-MoranNeutral0.14110.0033 ± 0.000220 ± 056.5732 ± 0.6597
PolyB2constant Wright-FisherAbundance0.89312770.0301 ± 1e-043.0543 ± 0.016559.9142 ± 0.0936
PolyB2constant Wright-FisherDriver0.00340.0034 ± 3e-0548.7328 ± 0.239656.3664 ± 0.0917
PolyB2constant Wright-FisherHybrid0.069980.0027 ± 2e-0550.3534 ± 0.240557.1445 ± 0.0928
PolyB2constant Wright-FisherNeutral0.03610.0026 ± 0.000140 ± 058.1592 ± 0.6741
Table 4
Model selection with selective pressure constrained to S = 1.
SampleGrowth ModelSelection ModelPPBF (Ho Neutral)PmissegSSteps
7Texponential pseudo-MoranAbundance0.27419e-04 ± 5e-051 ± 058.2452 ± 0.6646
7Texponential pseudo-MoranDriver0.23819e-04 ± 5e-051 ± 058.4745 ± 0.6725
7Texponential pseudo-MoranHybrid0.2619e-04 ± 5e-051 ± 058.586 ± 0.6668
7Texponential pseudo-MoranNeutral0.22819e-04 ± 6e-051 ± 058.5446 ± 0.6791
7Tconstant Wright-FisherAbundance0.25919e-04 ± 6e-051 ± 058.8089 ± 0.6627
7Tconstant Wright-FisherDriver0.2419e-04 ± 6e-051 ± 058.1783 ± 0.6771
7Tconstant Wright-FisherHybrid0.25719e-04 ± 5e-051 ± 059.0924 ± 0.6742
7Tconstant Wright-FisherNeutral0.24519e-04 ± 7e-051 ± 058.7516 ± 0.6787
U1Texponential pseudo-MoranAbundance0.27519e-04 ± 5e-051 ± 058.2452 ± 0.6646
U1Texponential pseudo-MoranDriver0.23919e-04 ± 5e-051 ± 058.4745 ± 0.6725
U1Texponential pseudo-MoranHybrid0.25819e-04 ± 5e-051 ± 058.586 ± 0.6668
U1Texponential pseudo-MoranNeutral0.22819e-04 ± 6e-051 ± 058.5446 ± 0.6791
U1Tconstant Wright-FisherAbundance0.25919e-04 ± 6e-051 ± 058.8089 ± 0.6627
U1Tconstant Wright-FisherDriver0.2419e-04 ± 6e-051 ± 058.1783 ± 0.6771
U1Tconstant Wright-FisherHybrid0.25719e-04 ± 5e-051 ± 059.1592 ± 0.6715
U1Tconstant Wright-FisherNeutral0.24519e-04 ± 7e-051 ± 058.7516 ± 0.6787
U2Texponential pseudo-MoranAbundance0.27610.0021 ± 8e-051 ± 057.3057 ± 0.653
U2Texponential pseudo-MoranDriver0.23510.0024 ± 0.000111 ± 057.7452 ± 0.6634
U2Texponential pseudo-MoranHybrid0.26410.0021 ± 7e-051 ± 058.1274 ± 0.654
U2Texponential pseudo-MoranNeutral0.22510.0024 ± 0.000111 ± 057.8758 ± 0.6772
U2Tconstant Wright-FisherAbundance0.26910.0023 ± 1e-041 ± 058.3439 ± 0.6532
U2Tconstant Wright-FisherDriver0.23310.0023 ± 9e-051 ± 057.4777 ± 0.693
U2Tconstant Wright-FisherHybrid0.26310.0023 ± 1e-041 ± 057.8662 ± 0.6683
U2Tconstant Wright-FisherNeutral0.23610.0025 ± 0.000121 ± 057.1433 ± 0.6655
U3Texponential pseudo-MoranAbundance0.27519e-04 ± 5e-051 ± 058.1624 ± 0.6643
U3Texponential pseudo-MoranDriver0.23919e-04 ± 5e-051 ± 058.4554 ± 0.6736
U3Texponential pseudo-MoranHybrid0.25819e-04 ± 5e-051 ± 058.586 ± 0.6668
U3Texponential pseudo-MoranNeutral0.22819e-04 ± 6e-051 ± 058.6178 ± 0.6777
U3Tconstant Wright-FisherAbundance0.25919e-04 ± 6e-051 ± 058.7611 ± 0.6614
U3Tconstant Wright-FisherDriver0.2419e-04 ± 6e-051 ± 058.1783 ± 0.6771
U3Tconstant Wright-FisherHybrid0.25719e-04 ± 5e-051 ± 059.0955 ± 0.674
U3Tconstant Wright-FisherNeutral0.24519e-04 ± 7e-051 ± 058.7516 ± 0.6787
14Texponential pseudo-MoranAbundance0.27519e-04 ± 5e-051 ± 058.1624 ± 0.6643
14Texponential pseudo-MoranDriver0.23919e-04 ± 5e-051 ± 058.4554 ± 0.6736
14Texponential pseudo-MoranHybrid0.25819e-04 ± 5e-051 ± 058.586 ± 0.6668
14Texponential pseudo-MoranNeutral0.22819e-04 ± 6e-051 ± 058.5446 ± 0.6791
14Tconstant Wright-FisherAbundance0.25919e-04 ± 6e-051 ± 058.8089 ± 0.6627
14Tconstant Wright-FisherDriver0.2419e-04 ± 6e-051 ± 058.1783 ± 0.6771
14Tconstant Wright-FisherHybrid0.25719e-04 ± 5e-051 ± 059.0924 ± 0.6739
14Tconstant Wright-FisherNeutral0.24519e-04 ± 7e-051 ± 058.7516 ± 0.6787
16Texponential pseudo-MoranAbundance0.27419e-04 ± 5e-051 ± 058.2452 ± 0.6646
16Texponential pseudo-MoranDriver0.23819e-04 ± 5e-051 ± 058.4745 ± 0.6725
16Texponential pseudo-MoranHybrid0.2619e-04 ± 5e-051 ± 058.586 ± 0.6668
16Texponential pseudo-MoranNeutral0.22810.001 ± 6e-051 ± 058.6274 ± 0.6789
16Tconstant Wright-FisherAbundance0.25919e-04 ± 6e-051 ± 058.8089 ± 0.6627
16Tconstant Wright-FisherDriver0.2419e-04 ± 6e-051 ± 058.1783 ± 0.6771
16Tconstant Wright-FisherHybrid0.25719e-04 ± 5e-051 ± 059.1051 ± 0.6742
16Tconstant Wright-FisherNeutral0.24519e-04 ± 7e-051 ± 058.7516 ± 0.6787
19Taexponential pseudo-MoranAbundance0.27310.0021 ± 8e-051 ± 057.4045 ± 0.6565
19Taexponential pseudo-MoranDriver0.24310.0024 ± 0.000111 ± 057.8025 ± 0.663
19Taexponential pseudo-MoranHybrid0.26110.0022 ± 8e-051 ± 057.9108 ± 0.65
19Taexponential pseudo-MoranNeutral0.22210.0025 ± 0.000121 ± 057.9331 ± 0.6777
19Taconstant Wright-FisherAbundance0.2710.0024 ± 0.000111 ± 058.2866 ± 0.6566
19Taconstant Wright-FisherDriver0.23310.0023 ± 1e-041 ± 057.8185 ± 0.6927
19Taconstant Wright-FisherHybrid0.26110.0023 ± 1e-041 ± 058.0478 ± 0.6705
19Taconstant Wright-FisherNeutral0.23710.0025 ± 0.000121 ± 057.2261 ± 0.6669
19Tbexponential pseudo-MoranAbundance0.27519e-04 ± 5e-051 ± 058.1624 ± 0.6643
19Tbexponential pseudo-MoranDriver0.23919e-04 ± 5e-051 ± 058.4554 ± 0.6736
19Tbexponential pseudo-MoranHybrid0.25819e-04 ± 5e-051 ± 058.586 ± 0.6668
19Tbexponential pseudo-MoranNeutral0.22819e-04 ± 6e-051 ± 058.5796 ± 0.6796
19Tbconstant Wright-FisherAbundance0.25919e-04 ± 6e-051 ± 058.7611 ± 0.6614
19Tbconstant Wright-FisherDriver0.2419e-04 ± 6e-051 ± 058.1178 ± 0.679
19Tbconstant Wright-FisherHybrid0.25719e-04 ± 5e-051 ± 059.1592 ± 0.6715
19Tbconstant Wright-FisherNeutral0.24519e-04 ± 7e-051 ± 058.7516 ± 0.6787
24Taexponential pseudo-MoranAbundance0.27519e-04 ± 5e-051 ± 058.1624 ± 0.6643
24Taexponential pseudo-MoranDriver0.23919e-04 ± 5e-051 ± 058.4554 ± 0.6736
24Taexponential pseudo-MoranHybrid0.25819e-04 ± 5e-051 ± 058.586 ± 0.6668
24Taexponential pseudo-MoranNeutral0.22819e-04 ± 6e-051 ± 058.6656 ± 0.6783
24Taconstant Wright-FisherAbundance0.25919e-04 ± 6e-051 ± 058.7611 ± 0.6614
24Taconstant Wright-FisherDriver0.2419e-04 ± 6e-051 ± 058.1783 ± 0.6771
24Taconstant Wright-FisherHybrid0.25719e-04 ± 5e-051 ± 059.1592 ± 0.6715
24Taconstant Wright-FisherNeutral0.24519e-04 ± 7e-051 ± 058.7516 ± 0.6787
24Tbexponential pseudo-MoranAbundance0.27310.0023 ± 0.000111 ± 057.0446 ± 0.6526
24Tbexponential pseudo-MoranDriver0.24210.0025 ± 0.000121 ± 057.551 ± 0.6661
24Tbexponential pseudo-MoranHybrid0.26410.0022 ± 9e-051 ± 057.9108 ± 0.6512
24Tbexponential pseudo-MoranNeutral0.22210.0026 ± 0.000131 ± 057.7516 ± 0.6758
24Tbconstant Wright-FisherAbundance0.26710.0024 ± 0.000131 ± 058.379 ± 0.6601
24Tbconstant Wright-FisherDriver0.23710.0024 ± 1e-041 ± 057.7357 ± 0.6922
24Tbconstant Wright-FisherHybrid0.25710.0023 ± 1e-041 ± 057.9045 ± 0.6718
24Tbconstant Wright-FisherNeutral0.23910.0025 ± 0.000121 ± 057.2643 ± 0.6726
26Nexponential pseudo-MoranAbundance0.27419e-04 ± 5e-051 ± 058.2452 ± 0.6646
26Nexponential pseudo-MoranDriver0.23919e-04 ± 5e-051 ± 058.4045 ± 0.6706
26Nexponential pseudo-MoranHybrid0.2619e-04 ± 5e-051 ± 058.586 ± 0.6668
26Nexponential pseudo-MoranNeutral0.22710.001 ± 7e-051 ± 058.6815 ± 0.6776
26Nconstant Wright-FisherAbundance0.25919e-04 ± 6e-051 ± 058.8089 ± 0.6627
26Nconstant Wright-FisherDriver0.23919e-04 ± 6e-051 ± 058.1783 ± 0.6771
26Nconstant Wright-FisherHybrid0.25719e-04 ± 5e-051 ± 059.1178 ± 0.6745
26Nconstant Wright-FisherNeutral0.24510.001 ± 7e-051 ± 058.6879 ± 0.6762
9Texponential pseudo-MoranAbundance0.27410.0021 ± 8e-051 ± 057.3854 ± 0.6574
9Texponential pseudo-MoranDriver0.24210.0024 ± 0.000111 ± 057.8025 ± 0.663
9Texponential pseudo-MoranHybrid0.26110.0022 ± 8e-051 ± 057.9108 ± 0.65
9Texponential pseudo-MoranNeutral0.22210.0025 ± 0.000121 ± 057.9522 ± 0.6787
9Tconstant Wright-FisherAbundance0.26910.0024 ± 0.000111 ± 058.2866 ± 0.6566
9Tconstant Wright-FisherDriver0.23310.0023 ± 1e-041 ± 057.9076 ± 0.6927
9Tconstant Wright-FisherHybrid0.26110.0023 ± 1e-041 ± 058.1115 ± 0.6708
9Tconstant Wright-FisherNeutral0.23610.0025 ± 0.000121 ± 057.2261 ± 0.6669
PolyB1exponential pseudo-MoranAbundance0.27410.0021 ± 8e-051 ± 057.4045 ± 0.6565
PolyB1exponential pseudo-MoranDriver0.24310.0024 ± 0.000111 ± 057.7102 ± 0.6622
PolyB1exponential pseudo-MoranHybrid0.26110.0022 ± 8e-051 ± 057.9459 ± 0.6512
PolyB1exponential pseudo-MoranNeutral0.22210.0025 ± 0.000111 ± 057.9522 ± 0.6776
PolyB1constant Wright-FisherAbundance0.27110.0023 ± 0.000111 ± 058.2834 ± 0.6575
PolyB1constant Wright-FisherDriver0.23110.0023 ± 9e-051 ± 057.6656 ± 0.6949
PolyB1constant Wright-FisherHybrid0.26110.0023 ± 1e-041 ± 057.9713 ± 0.6668
PolyB1constant Wright-FisherNeutral0.23710.0025 ± 0.000121 ± 057.207 ± 0.6674
PolyB2exponential pseudo-MoranAbundance0.27210.0027 ± 2e-041 ± 056.8471 ± 0.6544
PolyB2exponential pseudo-MoranDriver0.24510.0029 ± 0.000211 ± 057.3312 ± 0.6609
PolyB2exponential pseudo-MoranHybrid0.26310.0024 ± 0.000111 ± 057.9204 ± 0.6466
PolyB2exponential pseudo-MoranNeutral0.22110.0029 ± 0.000171 ± 057.4236 ± 0.6784
PolyB2constant Wright-FisherAbundance0.26810.0025 ± 0.000131 ± 058.2484 ± 0.6616
PolyB2constant Wright-FisherDriver0.23510.0026 ± 0.000141 ± 057.5796 ± 0.6897
PolyB2constant Wright-FisherHybrid0.25710.0026 ± 0.000151 ± 058.1115 ± 0.6741
PolyB2constant Wright-FisherNeutral0.2410.0027 ± 0.000141 ± 057.379 ± 0.6701
Table 5
Approximate reported per chromosome mis-segregation rates.
1st AuthorDOIModelTumor?StatisticAssessmentApproximate observed frequency %Aprrox modal chromosome # (ATCC)Approximate mis-segregation rate (per chromosome)
Bakhoumhttps://doi.org/10.1158/1078-0432.CCR-11-2049Tumor-TMATumorReportedLagging/Bridging31.3460.00680
Orrhttps://doi.org/10.1016/j.celrep.2016.10.030U2OSTumorApprox. MeanLagging32.5460.00707
Orrhttps://doi.org/10.1016/j.celrep.2016.10.030HeLaTumorApprox. MeanLagging22820.00268
Orrhttps://doi.org/10.1016/j.celrep.2016.10.030SW-620TumorApprox. MeanLagging22.5500.00450
Orrhttps://doi.org/10.1016/j.celrep.2016.10.030RPE1Non-tumorApprox. MeanLagging2.5460.00054
Orrhttps://doi.org/10.1016/j.celrep.2016.10.030BJNon-tumorApprox. MeanLagging8460.00174
Nicholsonhttps://doi.org/10.7554/eLife.05068AmniocyteNon-tumorApprox. MeanLagging0460.00000
Nicholsonhttps://doi.org/10.7554/eLife.05068DLD1TumorApprox. MeanLagging1460.00022
Dewhursthttps://doi.org/10.1158/2159-8290.CD-13-0285HCT116-DiploidTumorApprox. MeanLagging/Bridging23450.00511
Dewhursthttps://doi.org/10.1158/2159-8290.CD-13-0285HCT116-TetraploidTumorApprox. MeanLagging/Bridging50900.00556
Bakhoumhttps://doi.org/10.1038/ncb1809U2OSTumorReportedLagging460.01000
Zasadilhttps://doi.org/10.1126/scitranslmed.3007965CAL51TumorApprox. MeanLagging0.5440.00011
Thompsonhttps://doi.org/10.1083/jcb.200712029RPE1Non-tumorApprox. MeanAcute aneuploidy via FISH460.00025
Thompsonhttps://doi.org/10.1083/jcb.200712029HCT116-DiploidTumorApprox. MeanAcute aneuploidy via FISH450.00025
Thompsonhttps://doi.org/10.1083/jcb.200712029HT29TumorApprox. MeanAcute aneuploidy via FISH710.00250
Thompsonhttps://doi.org/10.1083/jcb.200712029Caco2TumorApprox. MeanAcute aneuploidy via FISH960.00900
Thompsonhttps://doi.org/10.1083/jcb.200712029MCF-7TumorApprox. MeanAcute aneuploidy via FISH820.00700
Bakhoumhttps://doi.org/10.1016/j.cub.2014.01.019HCT116-DiploidTumorApprox. MeanLagging6450.00133
Bakhoumhttps://doi.org/10.1016/j.cub.2014.01.019DLD1TumorApprox. MeanLagging2460.00043
Bakhoumhttps://doi.org/10.1016/j.cub.2014.01.019HT29TumorApprox. MeanLagging14710.00197
Bakhoumhttps://doi.org/10.1016/j.cub.2014.01.019SW-620TumorApprox. MeanLagging12500.00240
Bakhoumhttps://doi.org/10.1016/j.cub.2014.01.019MCF-7TumorApprox. MeanLagging17820.00207
Bakhoumhttps://doi.org/10.1016/j.cub.2014.01.019HeLaTumorApprox. MeanLagging13820.00159
Worrallhttps://doi.org/10.1016/j.celrep.2018.05.047BJNon-tumorApprox. MeanUnspecified Error5460.00109
Worrallhttps://doi.org/10.1016/j.celrep.2018.05.047RPE1Non-tumorApprox. MeanUnspecified Error5460.00109

Additional files

Transparent reporting form
https://cdn.elifesciences.org/articles/69799/elife-69799-transrepform1-v2.docx

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

  1. Andrew R Lynch
  2. Nicholas L Arp
  3. Amber S Zhou
  4. Beth A Weaver
  5. Mark E Burkard
(2022)
Quantifying chromosomal instability from intratumoral karyotype diversity using agent-based modeling and Bayesian inference
eLife 11:e69799.
https://doi.org/10.7554/eLife.69799