Dynamic readout of the Hh gradient in the Drosophila wing disc reveals pattern-specific tradeoffs between robustness and precision

Abstract
Editor's evaluation
Introduction
Results
Discussion
Materials and methods
Data availability
References
Article and author information
Metrics

Abstract

Understanding the principles underlying the design of robust, yet flexible patterning systems is a key problem in developmental biology. In the Drosophila wing, Hedgehog (Hh) signaling determines patterning outputs using dynamical properties of the Hh gradient. In particular, the pattern of collier (col) is established by the steady-state Hh gradient, whereas the pattern of decapentaplegic (dpp), is established by a transient gradient of Hh known as the Hh overshoot. Here, we use mathematical modeling to suggest that this dynamical interpretation of the Hh gradient results in specific robustness and precision properties. For instance, the location of the anterior border of col, which is subject to self-enhanced ligand degradation is more robustly specified than that of dpp to changes in morphogen dosage, and we provide experimental evidence of this prediction. However, the anterior border of dpp expression pattern, which is established by the overshoot gradient is much more precise to what would be expected by the steady-state gradient. Therefore, the dynamical interpretation of Hh signaling offers tradeoffs between robustness and precision to establish tunable patterning properties in a target-specific manner.

Editor's evaluation

This study presents a valuable finding on the precision conferred by dynamical interpretation of morphogen gradients. The evidence supporting the claims of the authors is convincing, with compelling theoretical analysis and solid experimental data. The authors have adequately addressed most concerns raised and so the work will be of considerable interest to the developmental biology and developmental systems biology communities.

https://doi.org/10.7554/eLife.85755.sa0

Introduction

Developmental patterning must be robust to variety of genetic and environmental perturbations in order to ensure a reproducible and functional body plan. Since patterns of gene expression are often specified by morphogen gradients, there has been considerable interest in understanding how these gradients reliably establish positional boundaries (Neumann and Cohen, 1997; Gurdon and Bourillot, 2001; Lander, 2007; Claret et al., 2007; Ibañes and Izpisúa Belmonte, 2008; Rogers and Schier, 2011; Li et al., 2018; Stapornwongkul et al., 2018). This reliability depends on the robustness of pattern specification with respect to different perturbations, as well as the precision or sharpness of pattern boundaries. Several theoretical studies have investigated the properties in which patterning robustness is ensured (Eldar et al., 2003; Bergmann et al., 2007; Lander et al., 2009; Adelmann et al., 2023). These studies are generally based solely on steady-state morphogen profiles and therefore, robustness applies equally to all patterning targets. As a result, steady-state morphogen gradients cannot tune these patterning properties in a target-specific manner. The Drosophila wing imaginal disc has become a useful system to study the mechanisms of morphogen formation and interpretation and offers testable patterning outputs in terms of both robustness and precision in the adult wing (Hartl and Scott, 2014; Restrepo et al., 2014; Chen and Zou, 2019). Along the anterior–posterior (AP) axis, the Drosophila wing is patterned by the Hedgehog (Hh) and Decapentaplegic (Dpp) morphogen gradients that determine the position of the longitudinal veins L2–L5 (Blair, 2007). Hh is produced in cells of the posterior compartment during the third larval instar and forms a short-range signaling gradient into the anterior compartment (Tabata and Kornberg, 1994). The Hh gradient organizes AP patterning of the wing both directly and indirectly; it defines adult patterning outcomes, such as the expression of the transcription factor knot or collier (col) which sets the distance between the longitudinal veins L3 and L4 (Vervoort et al., 1999; Anonymous, 2000); and the expression of decapentaplegic (dpp) in a domain broader than col (Basler and Struhl, 1994; Vervoort, 2000). While dpp does not have a direct patterning output in the adult wing, Dpp then acts as a long-range morphogen to globally coordinate patterning and growth along the AP axis (Affolter and Basler, 2007).

Contrary to other signaling pathways in which a ligand activates a signaling cascade by binding to its receptor, Hh signaling is activated by removing the receptor Patched (Ptc) from the plasma membrane, a process that is promoted by Hh binding and endocytosis (Torroja et al., 2005). This suggests that Hh signaling activity solely depends on the number of unbound Ptc receptors. However, a study suggested that the levels of Hh-bound Ptc can titrate the inhibitory effects of unbound Ptc and proposed that Hh signaling activity is more accurately represented by the ratio of bound to unbound Ptc receptor (Casali and Struhl, 2004). Importantly, an evolutionary conserved feature of the Hh signaling pathway is that ptc is itself a target of the signal. Since Ptc expression attenuates the dispersion and strength of signaling activity, Hh-dependent Ptc upregulation acts as a negative feedback that self-limits the range of the gradient (Chen and Struhl, 1996; Briscoe et al., 2001). This feedback property of Hh signaling results in self-enhanced ligand degradation which makes a narrower, but more robust gradient to perturbations in ligand dosage (Eldar et al., 2003; Lander et al., 2009).

Hh-dependent Ptc upregulation also provides an alternative interpretation of positional information, in which instead of using multiple concentration thresholds of the Hh steady state as in the classical morphogen model, patterning is established by interpreting positional information in a temporal manner using a single-threshold signaling range defined by a transient and the steady-state gradients (Nahmad and Stathopoulos, 2009). In particular, the boundary of dpp is established by an extended pre-steady-state gradient, known as the overshoot, while the anterior border of col is established by the steady-state gradient. Since the overshoot occurs prior to Hh-dependent Ptc upregulation, dpp should not exhibit the robustness property offered by the self-enhanced ligand degradation mechanism, but this has not yet been documented experimentally.

A study by Irons et al. compared the width of col expression in the wing disc as well as the L3–L4 intervein distance in adult wings of hh heterozygous and wild-type animals and found that they are not statistically different, supporting that some robustness to Hh dosage is exhibited by the system (Irons et al., 2010). Furthermore, Hatori et al. showed that the widths of col or ptc patterns do not significantly change in discs with 1, 2, 3, or 4 hh gene copies (Hatori et al., 2021). However, it remains unclear if the same robustness is exhibited by dpp which depends on the dynamics of the Hh gradient. By using mathematical modeling, here we show that when patterns are established by steady-state models of patterning all target genes exhibit the same robustness with respect to changes in morphogen production, in agreement with prior theoretical work (Eldar et al., 2003). However, when the Hh gradient is interpreted dynamically through the overshoot model (Nahmad and Stathopoulos, 2009), robustness to hh dosage becomes target specific. In particular, the specification of the anterior border of col is more robust than that of dpp, since the latter is independent of Hh-dependent Ptc upregulation. In contrast, we show that the anterior border of dpp model under the overshoot model offers increased precision, relative to what would be expected in the steady state only patterning model. Taken together, our work shows that the overshoot model of Hh signaling enables tunable robustness and precision properties in a target-specific manner. We discuss implications of this dynamic patterning model in the context of balancing reliability and flexibility during developmental patterning.

Results

Steady-state interpretation of morphogen gradients predicts identical robustness to morphogen dosage for all targets

Prior work on morphogen robustness has relied on quantifying displacements of the overall gradient shape (Gurdon and Bourillot, 2001; Tabata and Takei, 2004) or a single-threshold location of a gradient (Eldar et al., 2003). Robustness can be measured by computing the displacement ( $Δ x$ ) of the pattern boundary defined by a given morphogen threshold concentration, $T$ , as result of a specific perturbation:

Δ x = | x (T) - \tilde{x} (T) |,

where $x (T)$ and $\tilde{x} (T)$ are the positions defined by the concentration threshold $T$ of the unperturbed and perturbed morphogen gradients, respectively. Since Equation 1 is an absolute measure of robustness, in practice, perfect robustness occurs when $Δ x$ is less than the diameter of a single cell.

To investigate robustness of different target genes, we first analyze robustness predicted by classical morphogen models, that is, in which territories are defined by different thresholds of the steady-state gradient. As a starting model, we consider a free-diffusion, linear-degradation model at the steady state:

\frac{d^{2} M}{d x^{2}} - \frac{1}{λ^{2}} M = 0,

where $M$ is the concentration of the morphogen and $λ^{2}$ is the square of the characteristic gradient length, defined by the ratio between the diffusion coefficient and the degradation rate of the ligand $M$ , subject to the following boundary conditions:

\begin{array}{ll} B . C . 1. & M (0) = M_{0}, \\ B . C . 2. & lim_{x \to \infty} M (x) = 0. \end{array}

In this case, a perturbation in the morphogen source, $M_{0} \to {\tilde{M}}_{0}$ , results in a uniform displacement of the gradient which is given by $Δ x = λ \ln ({\tilde{M}}_{0} / M_{0})$ (Eldar et al., 2003), showing that patterns established by different thresholds exhibit the same response to this perturbation. This occurs because the solution of the perturbed problem is just a constant shift of the morphogen profile (Figure 1b–d).

Figure 1

Download asset Open asset

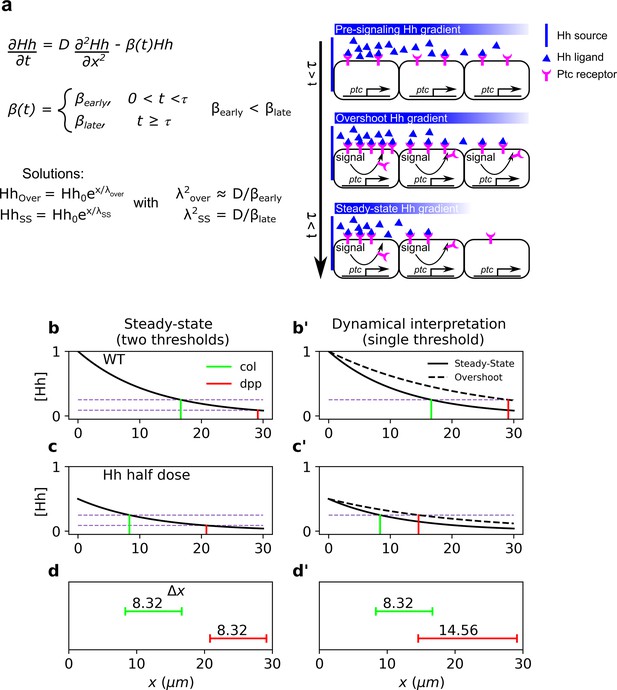
Dynamical interpretation model predicts differential robustness when morphogen dosage is reduced to half.

(a) Simple model of Hh signaling using a time-dependent step-wise degradation function. Diagrams displays a pre steady-state gradient that then retracts upon Hh-dependent *ptc* upregulation, resulting in a narrower gradient. (**b, c**) Plots of the analytical solution for the model in a using full ( $H h (x = 0) = 1$ ); (**b, b’**) or half ( $H h (x = 0) = 0.5$ ); (**c, c’**) Hh dosage. (**d, d’**) Displacements upon the above perturbation for the steady-state model with two thresholds (dotted horizontal lines corresponding to the locations of *col* and *dpp*) d; and for the dynamical interpretation model with a single-threshold readout (single dotted horizontal line) using the overshoot vs. the steady-state gradient predicts different shifts d’. The parameter values used for these plots are: $λ_{o v e r} = 21 μm$ , $λ_{S S} = 12 μm$ which approximately correspond to the anterior border positions of *col* and *dpp*, respectively. The color coding of *dpp* in red and *col* in green, will be used in the rest of the article.

Figure 1—source code 1 Code to generate Figure 1.: https://cdn.elifesciences.org/articles/85755/elife-85755-fig1-code1-v2.zip
Download elife-85755-fig1-code1-v2.zip

We then considered a very simple model of Hh signaling in the Drosophila wing. Since the expression of Ptc, the Hh receptor, is upregulated by Hh signaling and contributes to Hh degradation by binding the Hh ligand, we considered a model in which ligand degradation has different values within and beyond a presumptive Ptc expression domain:

\frac{\partial H h}{\partial t} = D \frac{\partial^{2} H h}{\partial x^{2}} + θ (x) α_{H h} - β (x, t) H h

where $θ (x) α_{H h}$ represents the source of Hh in the posterior compartment of the wing disc (i.e., $θ (x)$ is equal to 1 or 0, depending on whether $x$ is a location in the posterior [ $x < 0$ ] or anterior compartment [ $x > 0$ ], respectively), and

β (x, t) = γ_{H h_P t c} P t c + β_{H h},

where $γ_{H h_P t c}$ is the mass action constant for $H h_P t c$ binding. At the steady state, we expect that $P t c$ forms a uniform expression pattern over a stripe of anterior cells abutting the AP border (referred as $P t c_{s s}$ ) and away from the stripe, $P t c$ is expressed at basal levels, $P t c_{0}$ . Then, at the steady state $β_{steady-state} (x)$ can be modeled as the step function

β_{steady-state} (x) = {\begin{matrix} γ_{H h_P t c} P t c_{s s} + β_{H h}, & 0 < x < b, \\ γ_{H h_P t c} P t c_{0} + β_{H h}, & otherwise, \end{matrix}

where $b$ is the width of the Ptc stripe. For $x > 0$ , the steady-state solution of Equation 4 is given by

H h (x) = {\begin{matrix} H h_{stripe} (x) = A e^{x / λ_{2}} + B e^{- x / λ_{2}}, & 0 < x < b \\ H h_{beyondPtc} (x) = C e^{- x / λ_{1}}, & x \geq b . \end{matrix}

where $λ_{1}$ and $λ_{2}$ are the morphogens characteristic lengths within and beyond the Ptc stripe, and A, B, and C are constants determined by the boundary conditions. Upon a perturbation $α_{H h} \to {\tilde{α}}_{H h}$ , perturbed Hh concentrations are given by:

{\tilde{H h}}_{stripe} (x) = A e^{[x + \frac{1}{λ_{2}} \ln ⟮ \frac{{\tilde{α}}_{H h}}{α_{H h}} ⟯] / λ_{2}} + B e^{- [x - \frac{1}{λ_{2}} \ln ⟮ \frac{{\tilde{α}}_{H h}}{α_{H h}} ⟯] / λ_{2}},

and

{\tilde{H h}}_{beyondPtc} (x) = C e^{- [x - \frac{1}{λ_{1}} \ln ⟮ \frac{{\tilde{α}}_{H h}}{α_{H h}} ⟯] / λ_{1}} .

Note that once again, all territories defined by $H h_{beyondPtc}$ are shifted by the same amount, $λ_{1} \ln (\frac{{\tilde{α}}_{H h}}{α_{H h}})$ , upon variations in $α_{H h}$ . Therefore, any two target genes whose borders are defined by different concentration thresholds will exhibit the same robustness response.

Dynamic models of Hh signaling using a single threshold for different targets predict differential robustness

Previous work showed that Hh signaling in the Drosophila wing disc the anterior border of the Hh targets dpp and col are established by a single threshold at two time points during the formation of the Hh gradient; namely, at the overshoot and the steady state, respectively (Nahmad and Stathopoulos, 2009). To consider this dynamical patterning mechanism, we analyzed a simplified model which takes into accountx the temporal upregulation of ptc as a time-dependent switch function (Figure 1a). Following the overshoot model in Nahmad and Stathopoulos, 2009, we defined the overshoot gradient as the transient profile of maximum range. Since the timescale of Hh diffusion is much faster than the timescale of Ptc upregulation, we will assume that the Hh gradient reaches a pre-steady state with the first degradation rate, $β_{e a r l y}$ , where the anterior border of dpp is approximately defined and then the real steady state with the second degradation rate, $β_{l a t e}$ (Figure 1b’). Under this simple model of Hh signaling, the shift in patterning borders defined by the overshoot (i.e., dpp) and the displacement at the steady state are related by the following simple equation:

Δ x_{S S} = \frac{λ_{S S}}{λ_{o v e r}} Δ x_{o v e r},

where $λ_{o v e r}$ and $λ_{S S}$ are the morphogen characteristic lengths before and after ptc upregulation, respectively (see Figure 1a). Since $β_{e a r l y} < β_{l a t e}$ , then $λ_{S S} < λ_{o v e r}$ and $Δ x_{S S} < Δ x_{o v e r}$ , that is, overshoot-dependent targets are less robust than those established by the steady-state gradient. Then, in contrast to the steady-state model (Figure 1b–d), the overshoot model predicts differences in target gene displacement upon perturbation of morphogen dosages (Figure 1b’–d’), that is, robustness is target dependent, with higher robustness predicted for col patterning due to self-enhanced ligand degradation, than for dpp patterning (Figure 1d, d’). The ratio $λ_{S S} / λ_{o v e r}$ in Equation 10 may be written in terms of the kinetic parameters of Hh signaling (see Equation 6):

Δ x_{S S} = \frac{β_{o v e r}}{β_{S S}} Δ_{o v e r} = \frac{γ_{H h_P t c} P t c_{S S} + β_{H h}}{γ_{H h_P t c} P t c_{o v e r} + β_{H h}} Δ x_{o v e r} \approx \frac{P t c_{S S}}{P t c_{o v e r}} Δ x_{o v e r} .

The last approximation, which assumes that Ptc-dependent Hh degradation is much faster than other means of Hh degradation, provides an estimate of the difference in robustess for overshoot and steady-state targets as a function of Ptc levels. Note that in Equation 11, the difference in $Δ x$ between the steady state and overshoot model is independent of the specific threshold at which the Hh gradient establishes positional information. Thus, this equation provides a way to experimentally relate pattern robustness to actual patterning outputs in the system, such as Ptc expression levels (see Discusion).

We then asked if these results also hold in a more explicit model of the Hh pathway (Nahmad and Stathopoulos, 2009):

\frac{\partial H h}{\partial t} = D \frac{\partial^{2} H h}{\partial x^{2}} + S^{+} (x) α_{H h} - γ_{H h_P t c} H h \times P t c - β_{H h} H h,

\frac{\partial p t c}{\partial t} = S^{-} (x) α_{p t c 0} + \frac{α_{p t c} S i g n a l^{m}}{k_{p t c}^{m} + S i g n a l^{m}} - β_{p t c} p t c,

\frac{\partial P t c}{\partial t} = μ_{P t c} p t c - γ_{H h_P t c} H h \times P t c - β_{P t c} P t c,

\frac{\partial H h_P t c}{\partial t} = γ_{H h_P t c} H h \times P t c - β_{H h_P t c} H h_P t c,

\frac{\partial S i g n a l}{\partial t} = \frac{S^{-} (x) α_{S i g n a l} {(\frac{H h_P t c}{P t c})}^{n}}{k_{S i g n a l}^{n} + {(\frac{H h_P t c}{P t c})}^{n}} - β_{S i g n a l} S i g n a l,

where $H h$ , $p t c$ , $P t c$ , and $H h_P t c$ are the concentrations of Hh, ptc (mRNA), Ptc (protein), and the Hh-Ptc complex, respectively. The coefficients $α$ , $β$ , $γ$ , and μ represent the rates of synthesis, degradation, complex formation, and translation, respectively (see Figure 2-source data 6). We used a system of coordinates centered on the AP boundary with the anterior compartment on the negative side. $S^{+} (x)$ [alternatively, $S^{-} (x)$ ] is a step function of the form $S^{+} (x) = 1$ if $x > 0$ (alternatively, $S^{-} (x) = 1$ if $x < 0$ ) and zero otherwise. $S i g n a l$ represents the intracellular response of Hh signaling activity that activates target gene expression. The system of Equations 12–16 is subject to the following boundary and initial conditions:

\begin{array}{ll} I.C. 1 & p t c (x, 0) = S^{-} (x) \frac{α_{p t c 0}}{β_{p t c}}, \\ I.C. 2 & P t c (x, 0) = \frac{μ_{P t c}}{β_{P t c}} p t c (x, 0) = S^{-} (x) \frac{α_{p t c 0} μ_{P t c}}{β_{p t c} β_{P t c}}, \\ B. C. & {\frac{\partial H h}{\partial x} |}_{x = - 100} = {\frac{\partial H h}{\partial x} |}_{x = 100} = 0. \end{array}

We solved Equations 12–16 numerically and computed $Δ x$ (as in Equation 1) for the overshoot and steady-state $S i g n a l$ gradients upon a range of perturbations of the wild-type Hh production rate, $α_{H h_{0}}$ (Figure 2a). In agreement with our previous result (Figure 1), we found that the steady-state outputs are more robust than the overshoot outputs (Figure 2a). Moreover, this result holds independently of the specific choice of model parameters (Figure 2b). We conclude that higher robustness is predicted for targets specified by the steady-state gradient (col), with respect to those specified by the overshoot profile (dpp).

Figure 2

Download asset Open asset

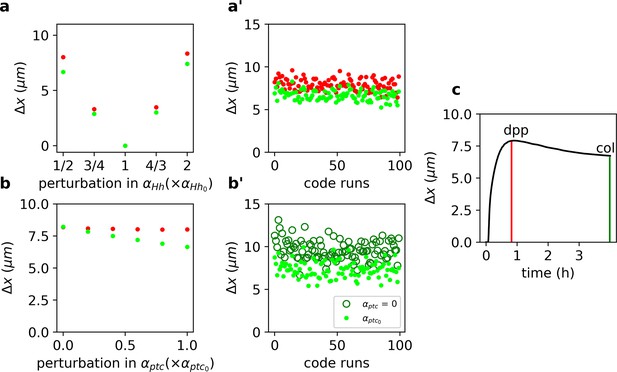
Target-specific robustness still holds in an explicit model of Hh signaling and it is dependent on Hh-dependent Ptc upregulation.

(a) $Δ x$ (defined as in Equation 1, but for the $S i g n a l$ function, see Materials and Methods) for overshoot (red) vs. steady-state (green) outputs upon different perturbations in $α_{H h}$ using the values of the parameters reported in Nahmad and Stathopoulos, 2009 (Figure 2—source code 2 and 3 and Figure 2—source data 1, 2, and 6). (a’) $Δ x$ defined and color coded as in a, for different combinations of parameter runs, when all parameters (other than $α_{H h}$ ) are varied through a random normal distribution around the mean value with a standard deviation of 10% of the mean value (Figure 2—source data 2). (b) Same as a, but for perturbations in $α_{p t c}$ (Figure 2—source data 3). (b’) Comparison of $Δ x$ for different parameters runs as in a’ for steady-state outputs (light green dots) and when $α_{p t c = 0}$ (dark green empty circles; Figure 2—source data 4). (c) $Δ x$ defined as in a, computed for the $S i g n a l$ gradient over time (Figure 2—source data 5). Red and green vertical lines indicate the overshoot and steady-state values corresponding to the anterior borders of *dpp* and *col*, respectively (Figure 2—source code 1).

Figure 2—source code 1 Code to generate Figure 2.: https://cdn.elifesciences.org/articles/85755/elife-85755-fig2-code1-v2.zip
Download elife-85755-fig2-code1-v2.zip
Figure 2—source code 2 Code to solve steady-state solution of Equation 18.: https://cdn.elifesciences.org/articles/85755/elife-85755-fig2-code2-v2.zip
Download elife-85755-fig2-code2-v2.zip
Figure 2—source code 3 Code to solve transient solution of Equations 12–17.: https://cdn.elifesciences.org/articles/85755/elife-85755-fig2-code3-v2.zip
Download elife-85755-fig2-code3-v2.zip
Figure 2—source data 1 Raw data to generate Figure 2a.: https://cdn.elifesciences.org/articles/85755/elife-85755-fig2-data1-v2.csv
Download elife-85755-fig2-data1-v2.csv
Figure 2—source data 2 Raw data to generate Figure 2a’.: https://cdn.elifesciences.org/articles/85755/elife-85755-fig2-data2-v2.csv
Download elife-85755-fig2-data2-v2.csv
Figure 2—source data 3 Raw data to generate Figure 2b.: https://cdn.elifesciences.org/articles/85755/elife-85755-fig2-data3-v2.csv
Download elife-85755-fig2-data3-v2.csv
Figure 2—source data 4 Raw data to generate Figure 2b’.: https://cdn.elifesciences.org/articles/85755/elife-85755-fig2-data4-v2.csv
Download elife-85755-fig2-data4-v2.csv
Figure 2—source data 5 Raw data to generate Figure 2c.: https://cdn.elifesciences.org/articles/85755/elife-85755-fig2-data5-v2.csv
Download elife-85755-fig2-data5-v2.csv
Figure 2—source data 6 Parameters used to solve Equations 12–17 (same values as in Nahmad and Stathopoulos, 2009).: https://cdn.elifesciences.org/articles/85755/elife-85755-fig2-data6-v2.csv
Download elife-85755-fig2-data6-v2.csv

Robustness of steady-state outputs depends on Hh-dependent Ptc regulation

Since previous work suggests that Hh-dependent ptc upregulation determines the range of the signal (Chen and Struhl, 1996), we wanted to confirm that Hh-dependent ptc regulation is responsible for the difference in robustness of Hh outputs. We perturbed the ptc production rate, $α_{p t c}$ , and noticed that $Δ x$ computed using the steady-state $S i g n a l$ profile is clearly reduced, but has little effect when computed with the overshoot $S i g n a l$ function (green vs. red dots in Figure 2b). Once again, this result is largely independent of the choice of parameters since robustness always improves compared to the case when $α_{p t c} = 0$ (Figure 2b’). Therefore, we suggest that Hh-dependent Ptc upregulation is responsible for differential robustness in this system by making steady-state outputs more robust with respect to overshoot-defined outputs.

Prior theoretical work suggests that when positional information is established before the steady state, it enhances robustness (Bergmann et al., 2007). This idea appears to contradicts our finding that overshoot-dependent patterning (which occurs prior to steady state) is less robust than steady-state-dependent patterning (Figure 2a, b). In order to understand the relative robustness of pre-steady-state gradients, we computed $Δ x$ , upon perturbations of $α_{H h}$ as a function of time in our model of Hh signaling. We found that early transient states exhibit the smallest $Δ x$ and therefore are the gradients that drive the more robust outputs, although they have a very limited range (Figure 2c), in agreement with the study of Bergmann et al., 2007. Then, $Δ x$ increases as the gradient approaches the overshoot when it reaches a maximum, before it starts to decrease again toward the steady state (Figure 2c).

col expression is more robust than dpp expression in the Drosophila wing disc

We then proceeded to test experimentally whether Hh targets are diferentially robust to changes in Hh dosage as predicted by the overshoot model. Previous studies showed that the width of the col domain is largely unaffected in hh heterozygous wing discs (Irons et al., 2010; Hatori et al., 2021). To investigate if this robustness property also holds for dpp, which is established by the overshoot (Nahmad and Stathopoulos, 2009), we examined the patterns of col (using a Col antibody) and dpp (using a dpplacZ reporter) in discs carrying 1 or 2 copies of hh (referred as hh(+/−) and hh(+/+), respectively). We found that the width of the Col pattern in hh(+/−) mutant discs is reduced by 1.66 $μm$ relative to hh(+/+) wild-type discs (Figure 3a, b, e). Although this difference is statistically significant, it is less than the average diameter of a single cell (about 2.5 μm) and therefore, it confirms previous experimental findings (Irons et al., 2010; Hatori et al., 2021). However, the pattern of dppLacZ is reduced by 4.44 μm in hh(+/−) discs relative to hh(+/+) controls (Figure 3c–e). This result does not depend on the size of the wing disc, since the pouch area in both, hh(+/−) and hh(+/+) discs are approximately the same (Figure 3—figure supplement 1), nor on the threshold used to measure the width of the patterns (see Figure 3—figure supplement 2). We conclude that, in agreement with the overshoot model of Hh signaling, but not with any of the steady-state models, the pattern width of Col is more robust than the pattern width of anterior dppLacZ.

Figure 3 with 2 supplements see all

Download asset Open asset

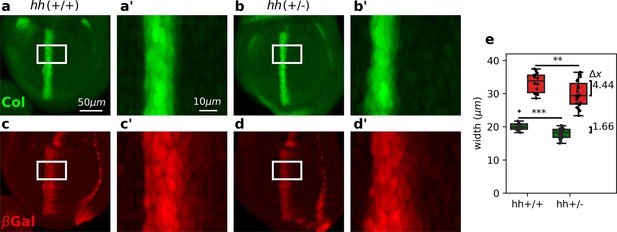
Differential robustness of Hh targets to hh dosage.

(**a-d**) Representative third-instar wild-type, hh(+/+) (**a, c**), and hh heterozygous hh(+/−) (**b, d**) wing discs immunostained with Col (**a, b**) and β-galactosidase (**c, d**) antibodies. Both hh(+/+) and hh(+/−) flies carry a transgene with a *dpp*LacZ enhancer trap, so β-galactosidase marks the pattern of *dpp* expression. The scale bars in a, a’ apply to b, b’; c, c’; and d, d’ panels, respectively. (a’**-d’**) Enlarged areas of the white boxes shown in (**a-d**). (e) Widths of the *col* and *dpp*LacZ patterns (color coded as in a–d) measured in the region marked by the white rectangle (see Figure 3—source data 1 and Figure 3—source code 1). The brackets on the right represent the difference between the medians of both groups. A non-parametric Mann–Whitney U test was applied in both cases (Figure 3—source data 1). Statistical p-values are $3.0 \times 10^{- 4}$ for Col (**) and $6.0 \times 10^{- 3}$ for *dpp*LacZ (***). hh(+/−) discs (n = 14). hh(+/+) discs (n = 23). See Figure 3—source code 1.

Figure 3—source code 1 Code to generate Figure 3.: https://cdn.elifesciences.org/articles/85755/elife-85755-fig3-code1-v2.zip
Download elife-85755-fig3-code1-v2.zip
Figure 3—source data 1 Raw data represented in Figure 3e .: https://cdn.elifesciences.org/articles/85755/elife-85755-fig3-data1-v2.csv
Download elife-85755-fig3-data1-v2.csv
Figure 3—source data 2 Raw data represented in Figure 3—figure supplement 1.: https://cdn.elifesciences.org/articles/85755/elife-85755-fig3-data2-v2.csv
Download elife-85755-fig3-data2-v2.csv

The overshoot model predicts higher precision in the establishment of the dpp border than would be expected from the classical steady-state model

Our findings that the width of dpp is less robust than the width of col in agreement with the overshoot model is puzzling. Why would Hh patterning uses a dynamic mechanism that patterns dpp at the time of least robustness (Figure 2c)? Why would col and dpp have different robustness properties (Figures 1d, 2a, and 3)? We wondered if this dynamical model trades off one patterning advantage over another in a target-specific manner. Morphogen concentrations are naturally noisy, which may cause territories to have a diffuse border especially when the morphogen narrowly declines due to self-dependent ligand degradation (Lander et al., 2009). In particular, we noticed that if dpp had to be specified by the steady-state gradient subject to Ptc-dependent degradation, instead that with the overshoot gradient, it would have to be specified at a location where the Hh gradient is nearly flat (Figure 4a). But at this same location, the Hh gradient is not as flat (Figure 4b). Therefore, we predicted that the overshoot model would establish a more precise dpp anterior boundary compared to a steady-state model, suggesting that the dynamic interpretation of Hh signaling would trade off robustness for precision. Therefore, we analyzed the performance of the overshoot and steady-state models at specifying the sharpness of a pattern boundary. We defined a measure of precision, $σ_{x}$ , for an experimental or simulated pattern boundary as the standard deviation of different measurements along the extension of the pattern (Figure 4c). Evidently, perfect precision occurs for $σ_{x} = 0$ , when the pattern would be completely sharp. In contrast, as $σ_{x}$ increases, the less precise the pattern boundary is.

Figure 4

Download asset Open asset

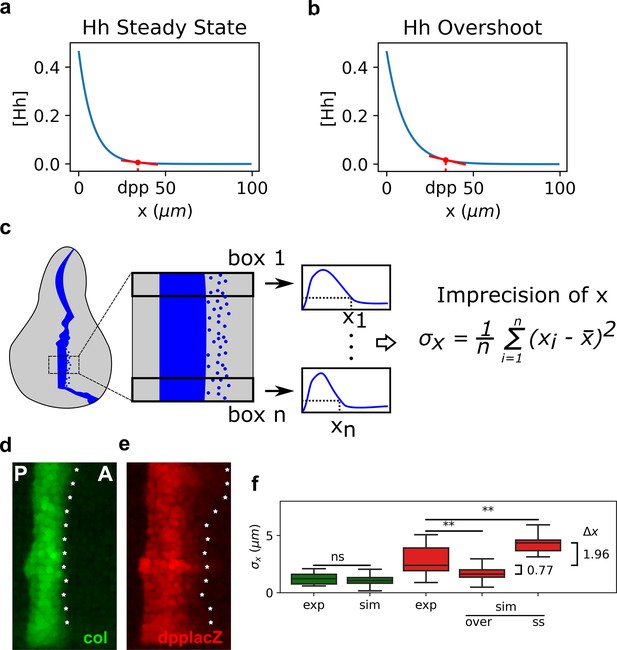
The overshoot model predicts more precision of the anterior border of *dpp* than the steady-state model.

(a, b). Representation of the steady-state (a) and overshoot (b) Hh gradients. At the location of the *dpp* anterior border, the slope of the gradient is steeper for the overshoot gradient than for the steady-state gradient. (c) Schematic representation of how we define our measure of precision for a patterning border (both in experimental and in simulated patterns). First, a box defines the region of interest (ROI) in the pattern. Then, this ROI is subdivided in $n$ boxes, each of which define a position $x_{i}$ . The measure of precision is the standard deviation of all the $x_{i}$ values. (d, e) Representative Col (d) and *dpp*LacZ (e) patterns in which the $x_{i}$ for each ROI as defined in c is measured and marked with an asterisk along the anterior border. (f) Quantification of $σ_{x}$ in several experimental (exp) and simulated (sim) patterns of *col* (green) and *dpp* (red). In the simulated patterns, noise levels are adjusted so that the distributions of *col* are not statistically significant and these noise levels are used to computed the simulated $σ_{x}$ of *dpp* as determined by the steady state (ss) or overshot (over) models. exp sample sizes as in Figure 3. sim sample sizes is n = 50 in all cases. For the statistical comparison, a Mann–Whitney U tests were applied in all cases. Statistical p-value for *col* was $p = 0.42$ . For experimental vs. overshoot *dpp*: $p = 1.0 \times 10^{- 3}$ (**), and for experimental vs. simulated steady-state *dpp*: $p = 9.0 \times 10^{- 3}$ (**).

Figure 4—source code 1 Code to generate Figure 4.: https://cdn.elifesciences.org/articles/85755/elife-85755-fig4-code1-v2.zip
Download elife-85755-fig4-code1-v2.zip
Figure 4—source data 1 Raw data represented in Figure 4f.: https://cdn.elifesciences.org/articles/85755/elife-85755-fig4-data1-v2.csv
Download elife-85755-fig4-data1-v2.csv

We first measured $σ_{x}$ at the anterior border of col and dpp in hh(+/+) wing discs reported in Figure 3. We found that col is about twice more precise than dpp (Figure 4d–f). Then, we compared the precision of the anterior border in simulated patterns of col and dpp (as defined both by the overshoot and steady-state gradients). To do so, we introduced Gaussian noise in the threshold $T$ at which the Signal function establishes a patterning position (see Materials and methods). Since the mechanism that sets the anterior border of the col pattern is the same in both the overshoot and steady-state interpretations, we fitted the extent of noise in the threshold $T$ such that the precision of the simulated border of col is the same as the one we measured in the experimental pattern ( $σ_{x}$ = 1.23 $μm$ ). At this extent of noise in $T$ , we compared the simulated border of $d p p$ defined by the overshoot ( ${d p p}_{o v e r}$ ) and steady-state models ( $d p p_{S S}$ ). We found that under the overshoot model, the anterior border of $d p p$ is predicted to be more precise than under the steady-state model (Figure 4f). Indeed, the overshoot model predicts a sharper border to what is observed experimentally, but this is not biologically significant since $σ_{x}$ is less than one cell diameter in both cases. However, the mean of $σ_{x}$ for the simulated dpp border under the steady-state model is 4.36 μm, suggesting that if the anterior border of dpp was established by a steady-state gradient, it would have an imprecision of approximately two cell diameters, which could have some patterning impact in the adult wing (see Discussion).

Discussion

The robust architecture of body plans to genetic and environmental perturbations is a general feature of developmental systems (Waddington, 1942; Csete and Doyle, 2002; Kitano, 2004). At the same time, this robust design should also admit some flexibility in order to allow the system to evolve and adapt under certain genetic or environmental challenges (Barkai and Shilo, 2007). While much work has been dedicated to the understanding of network features that confer robustness in developmental patterning, it is unclear how a robust, yet flexible architecture could be encoded in the interpretation of morphogen gradients (Lander et al., 2009; Lo et al., 2015). In particular, despite much prior theoretical work, the ability of a single morphogen to produce different patterning outputs with target-specific properties has not been studied in detail.

Relative to the classical view of morphogen interpretation, in which different morphogen concentration thresholds at the steady state define different borders of gene expression patterns, two strategies have been proposed to increase robustness to changes in the rates of morphogen production. First, morphogen gradients that promote their own degradation and sharply decay near the source of ligand production (Eldar et al., 2003). And second, gradients that specify patterns prior to steady state (Bergmann et al., 2007). When implementing either of these strategies, increased robustness is achieved for all gene expression patterns, regardless of the concentration thresholds at which they are established. However, both of these strategies have a clear inconvenience; they significantly narrow the patterning domain, and therefore, morphogen readout occurs where the gradient is essentially flat (Adelmann et al., 2023). Thus, these strategies provide robustness at the expense of a narrower gradient which may result in an imprecise border of gene expression. In agreement with this idea, Adelmann et al., 2023 recently showed that a linearly decaying gradient establishes more precise patterning boundaries with respect to a gradient established by a self-enhanced ligand degradation mechanism when interpreted several cells away from the morphogen source. The dynamic interpretation of Hh patterning in the Drosophila wing disc (Nahmad and Stathopoulos, 2009) offers a mechanistic implementation of this idea. First, a linearly decaying Hh gradient (the overshoot gradient) establishes the anterior border of dpp prior to upregulation of the Hh receptor, Ptc; once Ptc is upregulated, self-enhanced ligand degradation narrows the gradient and the anterior border of col is established (Figure 1). Under this model, the col border exhibits higher robustness than the dpp border to hh dosage (Figure 2), and our experimental data supports this prediction (Figure 3). This reduced robustness of dpp patterning occurs as a trade off for increased precision, relative to what would be expected by the steady-state interpretation model (Figure 4). Therefore, the dynamical interpretation of Hh signaling offers a target-specific, robust-yet-flexible architecture of patterning in this system (Figure 5).

Figure 5

Download asset Open asset

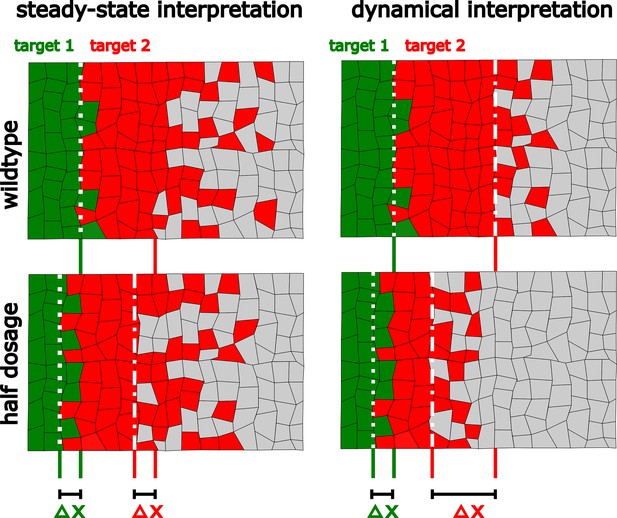
The dynamical interpretation of the Hh gradient trades off robustness for higher precision in a target-specific manner.

In the steady-state interpretation, all the target genes are established with the same robustness ( $Δ x$ ) upon perturbations in the amount of ligand. In the overshoot model interpretation one of the target genes (red) is established with less robustness than the other (green). However, it allows the less robust gene to be defined with greater precision than the steady state would define it (compare the sharpness of the boundaries of these patterns).

The finding that the displacement of the anterior borders of Hh targets is more than twice for dpp than for col ( $\approx 2.65$ , from their median values; Figure 3e) provides a interesting prediction about the overshoot gradient. From Equation 11, it can be inferred that the overshoot occurs when Ptc expressions is about twice its basal levels in the anterior compartment, but estimates suggest that Ptc reaches about seven times its basal levels in Ptc domain (Casali and Struhl, 2004). This suggests that the overshoot occurs significantly earlier than Ptc reaches its steady-state levels and that Ptc is produced at much larger amounts than what actually is needed to control the range of the Hh gradient. But since unbound Ptc represses Hh signaling, perhaps the purpose of building very high levels of Ptc is to desensitize Hh signaling over time as has been proposed for the vertebrate neural tube (Dessaud et al., 2008).

Why does this patterning system is wired to ensure robustness for the col border, but favors precision over robustness for dpp? In the Drosophila wing, the expression of col defines directly a specific feature in the adult wing, the L3–L4 intervein area (Vervoort et al., 1999), which corresponds to the more central area of the wing, whereas the dpp pattern does not have a direct positional role in the adult wing, but it acts as the source of another morphogen. As suggested by prior theoretical work, the source where a morphogen is produced does not have a significant impact on patterning (Mizutani et al., 2006), so the robustness of the dpp pattern may not subject to strong selection pressure during evolution, or perhaps other mechanisms downstream of Hh signaling exist to provide robustness at the level of Dpp signaling (Aguilar-Hidalgo et al., 2018; Romanova-Michaelides et al., 2022). In contrast, in the adult wing of Drosophila, precision could have a direct role on the sharpness of vein patterning. Thus, robustness ensures the correct positioning of veins whereas precision may be related to ensure straight veins. While it is unclear if a more imprecise dpp pattern would impact the straightness of veins 2 and 5 which are positioned by Dpp signaling, it suggests that in general, the overshoot model ensures robust positioning close to the morphogen source, but prioritize straightness of stripe-like patterns over positioning in more distant locations. Given that Ptc-dependent Hh degradation is evolutionary conserved (Chen and Struhl, 1996), our findings could have implications for robust and precise patterning in other systems as well.

Materials and methods

Key resources table

Reagent type (species) or resource	Designation	Source or reference	Identifiers	Additional information
strain, strain background (Drosophila melanogaster)	hh(+/−) allele	Bloomington Drosophila Stock Center	1749	ry[506] hh[AC]/TM3, Sb. hh[AC] is an amorphic allele
strain, strain background (Drosophila melanogaster)	dppLacZ	Bloomington Drosophila Stock Center	12379	cn[1] dpp[10638]/CyO; ry[506]. dpp[10638] is a lacZ is a dpp enhancer trap.
antibody	anti-Col (mouse monoclonal)	Gift from M. Crozatier Vervoort et al., 1999		1:250; overnight incubation
antibody	anti-β-gal (rabbit polyclonal)	MP Biomedicals	Cat. # 55976	1:250; overnight incubation
software, algorithm	Python	this paper	pandas; numpy; OpenCV; matplotlib; seaborn; odeint; solve_bvp	Customized source codes (available from this paper)

Fly stocks and crosses

Request a detailed protocol

Fly crosses were conducted at 25°C. For experiments using one copy of hh [hh(+/-)] (Figure 3), ry[506],hh[AC]/TM3,Sb[1] flies (Bloomington Drosophila Stock Center, BDSC, #1749) were crossed to cn[1],dpp10638/CyO (BDSC # 12379) flies at 25°C to obtain cn[1],dpp[10638]/ $+$ ; ry[506],hh[AC]/ry[506] discs. hh[AC] is a lost of function hh allele and dpp10638 is a transgene containing a LacZ reporter that drives nuclear β-galactosidase in the location of the dpp gene. Control discs with two copies of hh [hh(+/+)] are obtained from crossing the dppLacZ reporter stock to wild-type flies.

Wing imaginal disc dissection and immunostaining

Request a detailed protocol

Wing imaginal discs were dissected from third-instar larvae. Third-instar larvae were dissected under a stereoscopic microscope and fixed in PEM-T (PEM with 0.1% of Triton X-100) with 4% paraformaldehyde, washed three times, and blocked in PEM-T with 0.5% of bovine serum albumin for 2 hr at room temperature. Then, samples were stained with primary antibodies at 4°C overnight at the following dilutions: monoclonal mouse anti-Col (a gift from M. Crozatier, 1:250), rabbit anti-β-gal (MP Biomedicals, Cat. # 55976, 1:250). Primary antibodies were detected with Alexa Fluor 488 anti-mouse and Alexa Fluor 555 anti-rabbit secondary antibodies (1:1000). Imaging was done in a Leica TC5 SP8 confocal microscope using a 40× oil-immersion objective.

Numerical simulations

Request a detailed protocol

For computations in Figure 2, a Forward-in-Time-Centered-in-Space (FTCS) algorithm (using space and time steps of $1 μ m$ and time steps of $0.5 s$ , respectively) was implemented to solve Equations 12–16 in Python, using the parameters reported by Nahmad and Stathopoulos, 2009. At the steady state, the equations can be reduced to a single equation in each compartment (Nahmad and Stathopoulos, 2009):

D \frac{d^{2} H h_{S S}}{d x^{2}} + S^{+} (x) α_{H h} - \frac{χ S^{-} (x) H h_{S S}}{γ_{H h_P t c} H h + β_{P t c}} [α_{p t c 0} + \frac{α_{p t c} H h_{S S}^{n m}}{η^{m} ({k^{n} + H h_{S S}^{n}}^{m}) + S^{-} (x) H h_{S S}^{n m}}] - β_{H h} H h_{S S} = 0,

where

k = \frac{k_{S i g n a l} β_{H h_P t c}}{γ_{H h_P t c}},

η = \frac{k_{p t c} β_{S i g n a l}}{α_{S i g n a l}},

χ = \frac{μ_{P t c} γ_{H h_P t c}}{β_{p t c}} .

The steady-state Equation 18 was solved using solve_bvp and solve_ivp from scipy.integrate Python package. Plots were made with matplotlib and seaborn libraries of Python (see Figure 3—source code 1 and Figure 4—source code 1). To compute $Δ x$ as defined in Equation 1 in Figure 2, we used 0.2 of the maximum value of the $S i g n a l$ function and numerically solved for corresponding location $x$ .

For simulations of col and $d p p_{S S}$ patterns in Figure 4, we considered an exponential decay gradient of Hh, like obtained with the simple model in Figure 1, evaluated on a matrix of $80 \times 50$ . Patterns were determined by the position defined by the threshold $T$ of 20% of the maximum $S i g n a l$ value (with a Gaussian noise with mean $T$ and standard deviation determined in such a way that noise of simulated col coincides width background distribution noise of experimental col pattern, i.e., 1.23 μm). For $d p p_{o v e r}$ , we used numerical solution of $S i g n a l$ overshoot (i.e., the $S i g n a l$ function at the time of maximum range) to fit a Hill function, $A \frac{H h^{n}}{k^{n} + H h^{n}}$ , using the function fit_curve of scipy.optimize. We found $A = 0.2372$ , $k = 0.0483$ , and $n = 4.6212$ . Then, we used the approximation function of $S i g n a l$ overshoot to evaluate an exponential decay gradient of Hh overshoot and made an analysis analogous to what was done at the steady state. We measure the width of the pattern at 0.2 of the profile maximun obtained through a vertical projection of the simulated pattern.

Image analysis

Request a detailed protocol

For image analysis, we took the Z projection of the confocal images using ImageJ. 16-bit resolution images were saved in TIF format and then processed to measure the width of the fluorescence patterns using OpenCv library of Python. We normalized the intensity values after dividing them by the maximum intensity value and then we measured the width of each pattern domain at 0.2 of relative intensity (in Figure 3—figure supplement 2 we varied this threshold value from 0.1 to 0.6). Graphs were plotted with matplotlib and seaborn libraries of Python (see Source code for each panel of Figure 2). The same images were used to measure robustness (Figure 3) and precision (Figure 4).

Data availability

All data generated or analyzed during this study (including the source code) are included in this submission.

References

(2023) Patterning precision under non-linear morphogen decay and molecular noise
eLife 12:e84757.

https://doi.org/10.7554/eLife.84757
- PubMed
- Google Scholar
1. Affolter M
2. Basler K
(2007) The Decapentaplegic morphogen gradient: from pattern formation to growth regulation
Nature Reviews. Genetics 8:663–674.

https://doi.org/10.1038/nrg2166
- PubMed
- Google Scholar
(2018) Critical point in self-organized tissue growth
Physical Review Letters 120:198102.

https://doi.org/10.1103/PhysRevLett.120.198102
- PubMed
- Google Scholar
1. Anonymous J
(2000) Activation of knot (kn) specifies the 3–4 intervein region in the Drosophila wing
Development 127:55–63.

https://doi.org/10.1242/dev.127.1.55
- Google Scholar
1. Barkai N
2. Shilo BZ
(2007) Variability and robustness in biomolecular systems
Molecular Cell 28:755–760.

https://doi.org/10.1016/j.molcel.2007.11.013
- PubMed
- Google Scholar
1. Basler K
2. Struhl G
(1994) Compartment boundaries and the control of Drosophila limb pattern by hedgehog protein
Nature 368:208–214.

https://doi.org/10.1038/368208a0
- PubMed
- Google Scholar
1. Bergmann S
2. Sandler O
3. Sberro H
4. Shnider S
5. Schejter E
6. Shilo BZ
7. Barkai N
(2007) Pre-steady-state decoding of the Bicoid morphogen gradient
PLOS Biology 5:e46.

https://doi.org/10.1371/journal.pbio.0050046
- PubMed
- Google Scholar
1. Blair SS
(2007) Wing vein patterning in Drosophila and the analysis of intercellular signaling
Annual Review of Cell and Developmental Biology 23:293–319.

https://doi.org/10.1146/annurev.cellbio.23.090506.123606
- PubMed
- Google Scholar
1. Briscoe J
2. Chen Y
3. Jessell TM
4. Struhl G
(2001) A hedgehog-insensitive form of patched provides evidence for direct long-range morphogen activity of sonic hedgehog in the neural tube
Molecular Cell 7:1279–1291.

https://doi.org/10.1016/s1097-2765(01)00271-4
- PubMed
- Google Scholar
1. Casali A
2. Struhl G
(2004) Reading the Hedgehog morphogen gradient by measuring the ratio of bound to unbound Patched protein
Nature 431:76–80.

https://doi.org/10.1038/nature02835
- PubMed
- Google Scholar
1. Chen Y
2. Struhl G
(1996) Dual roles for patched in sequestering and transducing Hedgehog
Cell 87:553–563.

https://doi.org/10.1016/s0092-8674(00)81374-4
- PubMed
- Google Scholar
1. Chen Z
2. Zou Y
(2019) Anterior-posterior patterning of Drosophila wing discs I: a baseline mathematical model
Mathematical Biosciences 314:13–27.

https://doi.org/10.1016/j.mbs.2019.05.001
- PubMed
- Google Scholar
(2007) Evidence for a novel feedback loop in the Hedgehog pathway involving Smoothened and Fused
Current Biology 17:1326–1333.

https://doi.org/10.1016/j.cub.2007.06.059
- PubMed
- Google Scholar
1. Csete ME
2. Doyle JC
(2002) Reverse engineering of biological complexity
Science 295:1664–1669.

https://doi.org/10.1126/science.1069981
- PubMed
- Google Scholar
(2008) Pattern formation in the vertebrate neural tube: a sonic hedgehog morphogen-regulated transcriptional network
Development 135:2489–2503.

https://doi.org/10.1242/dev.009324
- PubMed
- Google Scholar
1. Eldar A
2. Rosin D
3. Shilo BZ
4. Barkai N
(2003) Self-enhanced ligand degradation underlies robustness of morphogen gradients
Developmental Cell 5:635–646.

https://doi.org/10.1016/s1534-5807(03)00292-2
- PubMed
- Google Scholar
1. Gurdon JB
2. Bourillot PY
(2001) Morphogen gradient interpretation
Nature 413:797–803.

https://doi.org/10.1038/35101500
- PubMed
- Google Scholar
1. Hartl TA
2. Scott MP
(2014) Wing tips: The wing disc as a platform for studying Hedgehog signaling
Methods 68:199–206.

https://doi.org/10.1016/j.ymeth.2014.02.002
- PubMed
- Google Scholar
(2021) Regulated delivery controls Drosophila hedgehog, wingless, and decapentaplegic signaling
eLife 10:e71744.

https://doi.org/10.7554/eLife.71744
- PubMed
- Google Scholar
1. Ibañes M
2. Izpisúa Belmonte JC
(2008) Theoretical and experimental approaches to understand morphogen gradients
Molecular Systems Biology 4:176.

https://doi.org/10.1038/msb.2008.14
- PubMed
- Google Scholar
1. Irons DJ
2. Wojcinski A
3. Glise B
4. Monk NAM
(2010) Robustness of positional specification by the Hedgehog morphogen gradient
Developmental Biology 342:180–193.

https://doi.org/10.1016/j.ydbio.2010.03.022
- PubMed
- Google Scholar
1. Kitano H
(2004) Biological robustness
Nature Reviews. Genetics 5:826–837.

https://doi.org/10.1038/nrg1471
- PubMed
- Google Scholar
1. Lander AD
(2007) Morpheus unbound: reimagining the morphogen gradient
Cell 128:245–256.

https://doi.org/10.1016/j.cell.2007.01.004
- PubMed
- Google Scholar
1. Lander AD
2. Lo W-C
3. Nie Q
4. Wan FYM
(2009) The measure of success: constraints, objectives, and tradeoffs in morphogen-mediated patterning
Cold Spring Harbor Perspectives in Biology 1:a002022.

https://doi.org/10.1101/cshperspect.a002022
- PubMed
- Google Scholar
1. Li P
2. Markson JS
3. Wang S
4. Chen S
5. Vachharajani V
6. Elowitz MB
(2018) Morphogen gradient reconstitution reveals Hedgehog pathway design principles
Science 360:543–548.

https://doi.org/10.1126/science.aao0645
- PubMed
- Google Scholar
1. Lo W-C
2. Zhou S
3. Wan FY-M
4. Lander AD
5. Nie Q
(2015) Robust and precise morphogen-mediated patterning: trade-offs, constraints and mechanisms
Journal of the Royal Society, Interface 12:20141041.

https://doi.org/10.1098/rsif.2014.1041
- PubMed
- Google Scholar
1. Mizutani CM
2. Meyer N
3. Roelink H
4. Bier E
(2006) Threshold-dependent BMP-mediated repression: a model for a conserved mechanism that patterns the neuroectoderm
PLOS Biology 4:e313.

https://doi.org/10.1371/journal.pbio.0040313
- PubMed
- Google Scholar
1. Nahmad M
2. Stathopoulos A
(2009) Dynamic interpretation of hedgehog signaling in the Drosophila wing disc
PLOS Biology 7:e1000202.

https://doi.org/10.1371/journal.pbio.1000202
- PubMed
- Google Scholar
1. Neumann CJ
2. Cohen SM
(1997) Long-range action of Wingless organizes the dorsal-ventral axis of the Drosophila wing
Development 124:871–880.

https://doi.org/10.1242/dev.124.4.871
- PubMed
- Google Scholar
(2014) Coordination of patterning and growth by the morphogen DPP
Current Biology 24:R245–R255.

https://doi.org/10.1016/j.cub.2014.01.055
- PubMed
- Google Scholar
1. Rogers KW
2. Schier AF
(2011) Morphogen gradients: from generation to interpretation
Annual Review of Cell and Developmental Biology 27:377–407.

https://doi.org/10.1146/annurev-cellbio-092910-154148
- PubMed
- Google Scholar
(2022) Morphogen gradient scaling by recycling of intracellular Dpp
Nature 602:287–293.

https://doi.org/10.1038/s41586-021-04346-w
- PubMed
- Google Scholar
(2018) Developmental biology: morphogen in a dish
Current Biology 28:R755–R757.

https://doi.org/10.1016/j.cub.2018.05.047
- PubMed
- Google Scholar
1. Tabata T
2. Kornberg TB
(1994) Hedgehog is a signaling protein with a key role in patterning Drosophila imaginal discs
Cell 76:89–102.

https://doi.org/10.1016/0092-8674(94)90175-9
- PubMed
- Google Scholar
1. Tabata T
2. Takei Y
(2004) Morphogens, their identification and regulation
Development 131:703–712.

https://doi.org/10.1242/dev.01043
- PubMed
- Google Scholar
(2005) Mechanisms of Hedgehog gradient formation and interpretation
Journal of Neurobiology 64:334–356.

https://doi.org/10.1002/neu.20168
- PubMed
- Google Scholar
(1999) The COE transcription factor Collier is a mediator of short-range Hedgehog-induced patterning of the Drosophila wing
Current Biology 9:632–639.

https://doi.org/10.1016/s0960-9822(99)80285-1
- PubMed
- Google Scholar
1. Vervoort M
(2000) hedgehog and wing development in Drosophila: a morphogen at work?
BioEssays: News and Reviews in Molecular, Cellular and Developmental Biology 22:460–468.

https://doi.org/10.1002/(SICI)1521-1878(200005)22:5<460::AID-BIES8>3.0.CO;2-G
- Google Scholar
1. Waddington CH
(1942) Canalization of development and the inheritance of acquired characters
Nature 150:563–565.

https://doi.org/10.1038/150563a0
- Google Scholar

Article and author information

Author details

Rosalío Reyes
1. Department of Physiology, Biophysics, and Neurosciences; Center for Research and Advanced Studies of the National Polytechnic Institute (Cinvestav), Mexico City, Mexico
2. Interdisciplinary Polytechnic Unit of Biotechnology of the National Polytechnic Institute, Mexico City, Mexico
Contribution
Conceptualization, Resources, Formal analysis, Validation, Investigation, Visualization, Methodology, Writing – original draft

Competing interests
No competing interests declared
Arthur D Lander

Department of Developmental and Cell Biology and Center for Complex Biological Systems, University of California, Irvine, Irvine, United States

Contribution
Conceptualization, Investigation, Methodology, Project administration, Writing – review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-4380-5525
Marcos Nahmad

Department of Physiology, Biophysics, and Neurosciences; Center for Research and Advanced Studies of the National Polytechnic Institute (Cinvestav), Mexico City, Mexico

Contribution
Conceptualization, Formal analysis, Supervision, Validation, Investigation, Methodology, Writing – original draft, Project administration

For correspondence
mnahmad@fisio.cinvestav.mx

Competing interests
Reviewing editor, eLife

"This ORCID iD identifies the author of this article:" 0000-0001-6300-5608

Funding

Centre for Research and Advanced Studies of the National Polytechnic Institute, Mexico (Institutional Support)

Marcos Nahmad

Consejo Nacional de Humanidades, Ciencias y Tecnologías (Graduate Fellowship)

Rosalío Reyes

National Institutes of Health (GM076516)

Arthur D Lander

The funders had no role in study design, data collection, and interpretation, or the decision to submit the work for publication.

Acknowledgements

We thank M Crozatier for kindly providing us with an aliquot of Collier antibody. We also thank Fanis Misirlis, José Antonio Arias, and members of the Nahmad laboratory for useful discussions, and Rafael Rodríguez-Muñoz and José Luis Fernández for technical assistance.

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.